Medidas para variables cualitativas
1. Proporción o frecuencia relativa: que es el número de casos que se presenta una característica (a) dividido por el número total de observaciones (a+b): a/(a+b). Su
valor oscila entre 0 y 1.
2. Razón o cociente: que es el número de casos que presentan una característica (a) dividido por el número de casos que no la presentan (b): (a/b).
3. Tasa: que es similar a la proporción, pero multiplicada por una cifra (por ejemplo 1.000, 10.000, 100.000) y se calcula sobre un determinado período de tiempo.
Introducción a la estadística básica para enfermería nefrológica
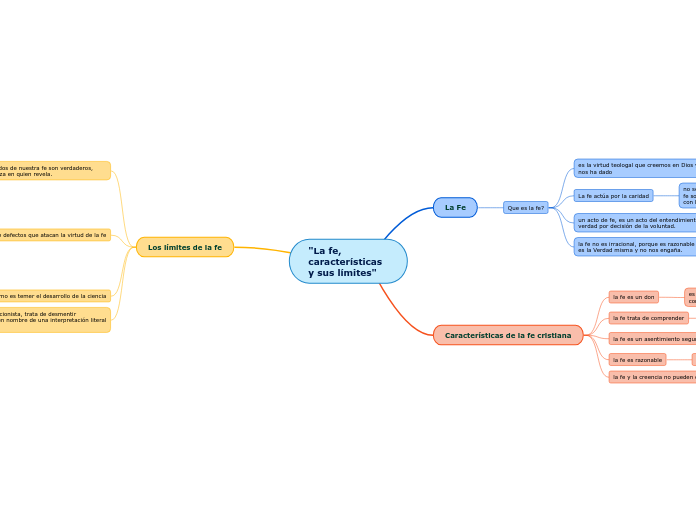
Pruebas de contraste de hipótesis. Errores Alfa y Beta
Error tipo I o α: el que se comete al rechazar la hipótesis nula H0, siendo cierta (se acepta que existen diferencias, cuando en realidad no las hay). La probabilidad de
cometer este error se conoce como a.
Error tipo II o ß: el que se comete al aceptar la hipótesis nula H0, siendo falsa (hay diferencia real, pero no se
acepta).
Hipótesis nula H0: supone que no hay diferencias entre los términos comparados. Las diferencias se deben sólo al azar.
Hipótesis alternativa H1: la que se acepta si H0 resulta rechazada. Supone que sí existen diferencias entre los términos comparados. Las diferencias no se deben al azar
Estimación de una población a partir de una muestra
El valor del EEM se calcula según la expresión siguiente: donde S =desviación estándar de la muestra n =número de individuos de la muestra EMM=S/√n
Estadística inferencial. Técnicas de Muestreo. Errores y Sesgos. Tamaño muestral
Errores y sesgos.
El error aleatorio es la diferencia entre el resultado, obtenido en la muestra y la realidad de la población. ERRORES SISTEMÁTICOS O SESGOS: Son errores que se cometen en el procedimiento del estudio,
Sesgos de selección: Las muestras no son adecuadamente representativas de la población de estudio. Sesgo de Berkson: las muestras
seleccionadas en un medio hospitalario pueden diferir sistemáticamente de las poblaciones generales.
Sesgos de seguimiento: Se cometen cuando no se observan por igual a ambos grupos, o si se pierden más individuos de un grupo que del otro (no al azar) a lo largo del estudio.
Sesgos de información: Se cometen al recoger las medidas o datos Sesgos de confusión: Son los producidos por la existencia de factores o variables de confusión.
Tamaño de la muestra
Para su cálculo se precisa la definición previa de los riesgos a asumir: los errores tipo I o alfa y II o beta, y la magnitud de la diferencia que se desea detectar
Técnicas de muestreo.
Muestreo aleatorio simple: se utilizan números aleatorios extraídos de unas tablas o generadas por ordenadores. En muestras pequeñas puede no representar adecuadamente a la población. Muestreo estratificado: La población se divide ensubgrupos o estratos, y después se obtiene una muestra
aleatoria de cada uno de ellos.
Muestreo sistemático: Se aplica una regla simple fija para el muestreo, de modo que se divide el total de la
población de estudio entre el tamaño de la muestra, hallando así una constante de muestreo, k.
Muestreo en etapas múltiples: Consiste en seleccionar unidades de muestreo de una población (unidades primarias) y obtener en una segunda etapa una muestra de cada una de ellas (unidades secundarias).
Muestreo no probabilístico: En este caso se utilizan métodos en los que no participa el azar.
Distribuciones de probabilidad. La distribución norma
Distribución normal o de Gauss: Es la distribución de probabilidad teórica más importante. Distribución binomial: Cuando la variable sólo tiene dos valores posibles, se dice que sigue una distribución binomial. Distribución de Poisson: La distribución discreta de Poisson se utiliza para determinar la probabilidad de que un suceso raro ocurra un determinado número de veces, cuando el número de ensayos es
grande y la probabilidad de que aparezca el suceso es pequeña.
Estadística descriptiva, presentación de los datos
La estadística descriptiva es la rama de la estadística que recolecta, analiza y caracteriza un conjunto de datos, con el objetivo de describir las características y comportamientos mediante medidas de resumen, tablas o gráficos.
Histograma: Se utiliza para variables cuantitativas continuas. Polígono de frecuencias: se construye uniendo los puntos medios de la zona más alta de los rectángulos. Diagrama de barras: Se utiliza para variables cualitativas y cuantitativas discretas. Gráfico sectorial o pastel: un círculo
representa el total, y un segmento o porción del pastel es la proporción o porcentaje de cada categoría de la variable.
Síntesis de los datos
Medidas de centralización
Recorrido o rango: Es la diferencia entre los valores máximo y mínimo de la variable. Recorrido intercuartil: también llamado media de dispersión. Se calcula dividiendo en primer lugar los datos (previamente ordenados) en cuatro partes iguales, obteniendo así los cuartiles Q1, Q2,y Q3; la diferencia entre el cuartil Q3 y el Q1 es el recorrido intercuartil, y abarca el 50% de los datos. Desviación media, Varianza (S2) y desviación estándar (S o DE): Se basan en cálculos de la diferencia entre cada valor y la media aritmética (x-x). La diferencia entre las tres medidas es cómo se prescinde del signo negativo: en la desviación media, se toman los valores absolutos |x-x|; en la varianza (S2 para muestras y σ2 para poblaciones) se eleva al cuadrado la diferencia: (x-x)2. coeficiente de variación: Se calcula dividiendo la DE por la
media, multiplicando después por 100.
Media: También llamada promedio, se calcula sumando todos los valores observados y dividiendo por el número de observaciones de la muestra. Se representa como x. Moda: Valor que más veces se repite, pueden existir
varias modas en un conjunto de datos. Mediana: Valor central cuando los datos están ordenados, si el número de datos es impar será el valor
del centro y si es par será el promedio de los valores centrales. Cuartiles, Deciles, Percentiles: localizan otros puntos
de una distribución. Los cuartiles dividen los datos en cuatro partes iguales, los deciles en diez partes iguales y los percentiles, en cien partes iguales.
Población, muestra, individuo, variables y tipos de variables
Las variables o caracteres son las propiedades o características que se estudian en cada individuo de la muestra,
Variables dependientes: son el objeto de interés, que varía en respuesta a alguna intervención.
Variables independientes: es la intervención, o lo que está siendo aplicado. Variables cualitativas, que tienen valores no numéricos (sexo, religión, color de los ojos). Variables cuantitativa,que son aquellas que toman
valores numéricos (glucemia, número de hijos, peso,coeficiente intelectual).
muestra es un conjunto menor de individuos, accesible y limitado. Cada uno de los componentes de la población y de la muestra se denomina individuo. Al número de individuos que forman la muestra se llama tamaño, y se representa con la letra n.
población se define como un conjunto homogéneo de individuos que generalmente es inaccesible para su estudio al ser de un tamaño inabordable.
Estadística en ciencias de la salud y tipos de estadística
La estadística descriptiva compren-
de la presentación, organización y resumen de los datos de una manera científica. La estadística inferencial o inductiva permite generalizar los datos obtenidos a partir de una muestra a un número mayor de individuos (población).
La estadística es una ciencia,basada en las matemáticas. por ejemplo, Cuando hablamos de la dosis media de eritropoyetina administrada en diálisis o el tiempo medio de duración de una sesión de hemodiálisis estamos utilizando la estadística.