DEFINIZIONE : La disequazione e' una diseguaglianza che e' verificata per certi intervalli di valori
Ad esempio la disequazione
x - 4 0
e' verificata per tutti i valori della x maggiori di 4, cioe' se al posto della x metto 5, 6, oppure 4,111... e' vero che il primo termine della disuguaglianza e' maggiore o uguale al secondo
Risolvere una disequazione significa trovare gli intervalli dei valori che sostituiti alla x rendono la diseguaglianza vera
In una disequazione possiamo trovare solo i valori maggiori oppure minori di qualcosa
oppure possiamo trovare i valori maggiori e uguali oppure minori e uguali .
Occorre fare molta attenzione e considerare sempre se devo o no prendere il valore corrispondente all'uguale
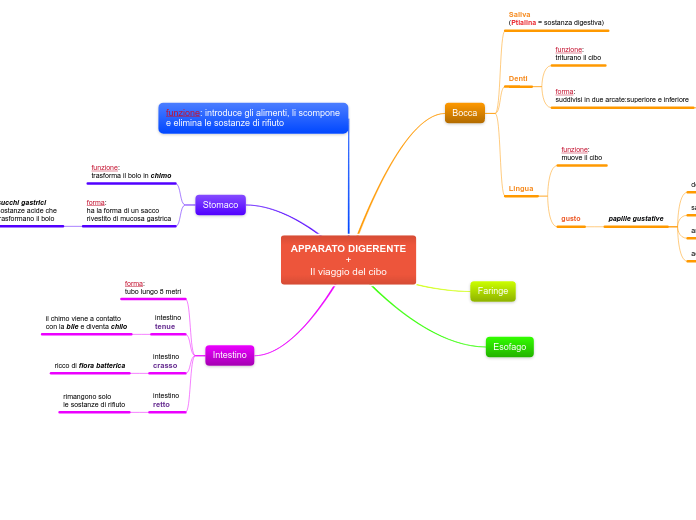
DOMINIO: Si dice dominio di una funzione f(x) l'insieme dei valori possibili che la variabile indipendente x può assumere, in modo che la funzione sia definita in tali valori.
le funzioni
Cognome: Riascos
Nome: Marcela
Classe: IV s
Anno Scolastico: 2015/2016
scuola: Ipsia A. Castigliano
Grafico
DERIVATA PRIMA
STUDIO DI FUNZIONE
Continuità
ASINTOTI
Asintoto è una retta a cui tende una funzione in un comportamento limite.
Vi sono tre tipi di asintoti:
LIMITI
CALCOLO DEI LIMITI
SEGNO
PARI E DISPARI
Una funzione si dice DISPARI se assume valori apposti in corrispondenza con due ascisse opposte nel dominio DD
Una funzione si dice PARI se assume lo stesso valore in corrispondenza di due ascisse opposte nel suo dominio DD
CODOMIONIO
DOMINIO
Esempio
Funzione matematica: ci sono due insiemi: -A, formato dagli elementi a,b,c,d e l'insieme B formato dagli elementi e,f,g,h. L'elemento A è associato ad un SOLO elemento della B.
Funzione non matematica
esempi
Link utili
Video
Sottoargomento
Tipologie di funzione
FUNZIONI ALGEBRICHE: Compaiono solo operazioni di tipo algebrico.
FUNZIONI TRASCENDENTI: Sono tutte quelle funzioni che NON sono algebriche, si dividono in:
Esponenziale: Si dice esponenziale una funzione che si presenta nella forma Y=a² dove a è un numero reale, positivo e diverso da 1
Lineare: si chiama lineare la funzione del tipo: Y=mx + q, m e q sono numeri fissati e il grafico di questa funzione sarà una retta.
Logaritmica: la funzione è l'inversa dell'esponenziale, pertanto dominio e codomio risultano scambiati rispetto a quelli della funzione esponenziale. Y=Logx
Goniometriche:
DEFINIZIONE: E' una relazione tra due insieme A e B che associa ad un elemento X £ A uno e un solo elemento Y £ B