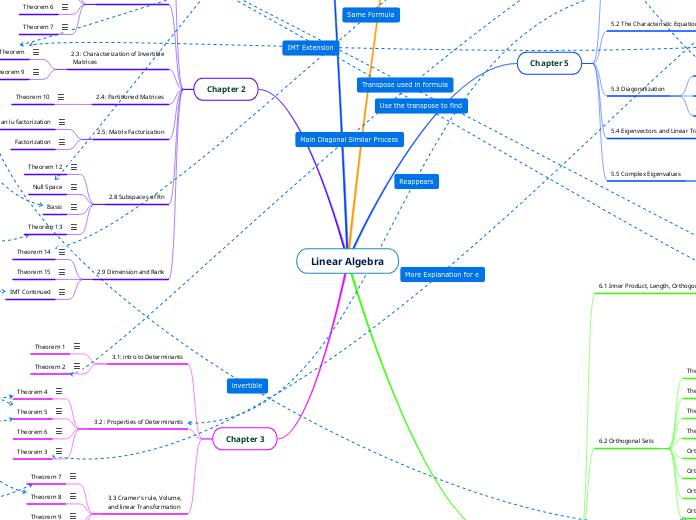
Linear Algebra
Chapter 6
6.7 Inner Product Spaces
Theorem 17
The Triangle inequality
for all u,v, in V
||u+v||<= ||u||+||v||
Theorem 16
The cauchy-schwartz inequality
for all u, v in v
|<u,v>|<= ||u||||v||
Lengths, Distances, and Orthogonality
Let V be an inner product space, with the inner product denoted by <u,v> just as in R^n we define the length of a vector to be scalar
||v|| = √<v , v>
Equivalently, ||v||^2 = <v,v>
a unit vector is one whose length is 1. The distance between u and v is ||u-v||. Vectors u and v are orthogonal if <u,v>=0
Inner Product space
An inner product on a vector space v is a function that, to each pair of vectors u and v in V, associates a real number <u,v> and satisfies the following axioms for all u,v and w in V and all scalars c.
a. <u ⋅ v> = <v ⋅ u>
b. <u+v,w> = <u,w> +< v,w>
c. <cu , v > = c<u,v>
d. <u ,u> ≥ 0 and <u , u > = 0 if and only if u = 0
A vector space with an inner product is called an inner product space
6.5 Least Squares Problems
Least-squares solution
if A is m * n and b is in R^M a least square solution of Ax=b is an xhat in R^n such that
||b-A(xhat)|| <= ||b-Ax||
for all x in R^n
Given an m * n matrix A with linearly independent columns let A =QR be a QR factorization of A as in Theorem 12. Then for each b in r^m, the equation Ax = b has a unique least squares solution given by
x(hat) = (R^-1)(Q^T)b
Let A be an m * n matrix. The following statements are logically equivalent
a. the equations Ax= b has a unique least-square solution for each b in R^m
b. The columns of A are linearly independent
c. The matrix A^t A is invertiable
When these statements are true the least square solution xhat is given by
xhat =(A^TA)^-1A^tb
THe set of least squares solutions of Ax =b coincides with the nonempty set of solutions of the normal equations (A^t)AX = (A^T)b
6.4 Gram-Schmidt Process
If a is an m * n matrix with linearly independent columns, then A can be factored as A = QR where Q is an m * n matrix whose columns form an orthonormal basis for col A and R is an n * n upper triangular invertible matrix with positive entries on its diagonal
Given a basis {x1 ... x2} for a nonzero subspace w of R^n define
v1= x1
v2= x2 - ((x2⋅v1)/(v1⋅v1))v1
v3= x3 - ((x3⋅v1)/(v1⋅v1))v1 - ((x3⋅v2)/(v2⋅v2))v2
vp= x3 - ((xp⋅v1)/(v1⋅v1))v1 - ((xp⋅v2)/(v2⋅v2))v2 .. -((xp⋅vp-1)/(vp-1⋅vp-1))vp-1
then {v1....vp} is an orthogonal basis for w in addition
span {v1....vp} = span {x1 ... xk} for 1 <= k <= p
6.3 Orthogonal Projects
Properties of orthogonal projection
If {u1 ... up} is an orthogonal basis for W and if y happens to be in w then the formula for projw y is exactly the same as the representation of y given in theorem 5 in this case projw y =y
If {u1....up} is an orthonormal basis for a subspace w of R^n then
projwy= (yu1)u1+(yu2)u2+......+(yup)up
if u =[u1u2...up] then projwy=u(u^t)(y) for all y in R^n
Best Approximation theorem: Let W be a subspace of R^n let y be any vector in R^n and let yhat be the orthogonal projection of y onto w, the yhat is the closet point in w to y in the sense that
||y-yhat||<||y-v||
for all v in w distinct form yhat
Le W bea subspace of R^n. Then each y in r^n can be written uniquely in the form.
y= yhat + z
where yhat is in w and z is in w^⊥ in fact if {u1..... up} is any orthogononal basis of w then
yhat =(y⋅u1)/(u1⋅u1)u1 + .... + yhat =(y⋅up)/(up⋅up)up
and y=y-yhat
6.2 Orthogonal Sets
Orthogonal Matrix
a square matrix u such that u^-1 = U^T
Orthonormal Sets
A set {u1 ... up} is an orthonormal set if it is an orthogonal set of unit vectors. if W is the subspace spanned by such a set, then {u1 . . . up} is an orthonormal basis for W, since the set is automatically linearly independent, by theorem 4
Orthogonal Projection
decomposing a vector y in r^n into the sum of two vectors one a multiple of u and the other orthogonal to u
y =yhat + z
yhat = αu for some scalar α and z is some vector orthogonal to u let z = y-αu then y-yhat is orthogonal to u if and only if
0= (y-αu)⋅u = y⋅u-(αu)⋅u=y⋅u-α(u⋅u)
α=(y⋅u)/(u⋅u) and yhat =(y⋅u)/(u⋅u)
The vector y hat is called the orthogonal projection of y onto u and the vector z is called the component of y orthogonal to u
yhat= projly = (y⋅u/u⋅u)u
Orthogonal Basis
An orthogonal basis for a subspace w of R^n is a basis for w that is also an orthogonal set
Let U be an m * n matrix with orthonormal columns, and let x and y be in R^n then
a. ||Ux|| = ||x||
b. (Ux) * (Uy) = x⋅y
c. (Ux) * (Uy) = 0 if and only if x⋅y = 0
An m * n matrix U has orthonormal columns if and only if u^Tu = 1
let {u1....up} be an orthogonal basis for a subspace w of R^n for each y in W the weights in the linear combination
y = c1u1+...+cpup
are given by
cj = y⋅uj/uj⋅uj (j=1,....p)
If S = {u1....up} is an orthogonal set of nonzero vectors in R^n then s is linearly independent and hence is a basis for the subspace spanned by s
6.1 Inner Product, Length, Orthogonality
Orthogonal
Two vectors u and v in R^n are orthogonal to each other if
u ⋅ v = 0
Distance
For u and v in R^n and the distance between u and v written as dist(u,v) is the length of the vector u-v that is.
dist(u,v) = || u- v ||
Length/Norm
The length (or norm) of v is the nonnegative scalar ||v|| defined by
||v||=√(v ⋅ v) = √(v1^2+v2^2+...+Vn^2)
and
||v|| = v ⋅ v
Dot Product
If u and v are vectors R^n then we regard u and v as n * 1 matrices. The transpose u^t is a 1 * n matrix, and the matrix product u^(t)v is a 1 * 1 matrix which we write as a single real number without brackets. the number u^t(v) is called the inner product of u an v often written as u ⋅ v
Let A be an m * n matrix. THe orthogonal complement of the row space of A is the null space of A and the orthogonal complement of the column space of A is the null space of A^t
(row A) = Nul A and (col A) = nul A^T
Two vectors u and v are orthogonal if and only if
||u+v||^2 = ||u||^2+ ||v||^2
Let u, v, and w be vectors in R^n and let c be scalar then
a. u ⋅ v = v ⋅ u
b. (u+v)⋅w = u⋅w + v⋅w
c. (cu) ⋅ v = c(u⋅v) = u ⋅ (cv)
d. u ⋅ u ≥ 0 and u ⋅ u = 0 if and only if u = 0
Chapter 5
5.5 Complex Eigenvalues
Let A be a real 2 * 2 matrix with a complex eigenvalue λ =a-bi(b=/=0) and an associated eigenvector v in c^2 then
A=PCP^-1 where p = [Re v im V] and c= [a -b]
[b a]
Real and imaginary Parts of Vectors
The Complex conjugate of a complex vector x in C^n is the vecto x in c^n whose entries are the complex conjugates of the entries in x. The real and imaginary parts of a complex vector x are the vectors re x and im x in R6n formed from the real and imaginary parts of the entries of x thus
x= rex+ilmx
(Complex)eigenvalues/eigenvectors
The matrix eigenvalues-eigenvector theory already developed for r^n applies equally well to c^n. so a complex scalar λ satisfies det(a - λI) = 0 if and only if there is a nonzero vector x in c^n such that Ax = λx. We call λ a (complex) eigenvalue and x (complex eigenvector corresponding to λ.
5.4 Eigenvectors and Linear Transformations
Diagonal Matrix Representation
Suppose A=PDP^-1 where D is a diagonal n*n matrix. If B is the basis for R^n formed from the columns of P, then D is the B-matrix for the transformation x->Ax
Matrix for t relative to the basis B
Formula
M= [[T(b1)]b[T(b2)]b.....[T(bn)]b]
5.3 Diagonalization
Let A be an n*n matrix whose distinct eigenvalues are λ1....λp
A. For 1<=k<= p the dimension of the eigenspace for λk is less than or equal to the multiplicity of the eigen value λk
b. The matrix A is diagonalizable if and only if the sum of the dimensions of the eigenspace equals n and this happens if an only if 1. the characteristics polynomial factors completely into linear factors and 2. the dimensions of the eigenspace for each λk equal the multiplicity of λk
C. If A is diagonalizable and bk is a basis for the eigenspace corresponding to λk for each k, then the total collection of vectors in the set b1 ... bp forms an eigenvector basis for R^n
An n *n matrix with n distinct eigenvalues is diagonalizable
The Diagonalization Theorem
an n*n matrix A is diagonalizable if and only if A has n linearly independent eigenvectors
In fact A = PDP^-1 with D a diagonal matrix if and only if the columns of P are linearly independent eigenvectors of A. In this case, the diagonal entries of D are eigenvalues of A the correspond respectively to the eigenvectors in P
5.2 The Characteristic Equation
Let A be an n*n matrix Then A is invertible if and only if
r. The number 0 is not an eigenvalue of A
If n * n matrices A and B are similar then they have the same characteristic polynomial and hence the same eigenvalues
Properties of Determinants
Let A and B be n*n matrices
a. A square matrix A is invertible if and only if det A =/= 0
b. det Ab= (detA)(Det B)
c. det A^t = det A
d. If A is a triangular matrix, then det A is the product of the entries on the main diagonal of A
e. A row replacement operation does not change the determinant
5.1 Eigenvectors and Eigenvalues
Eigenvalue
A scalar λ is called an eigenvalue of A if there is a nontrivial solution x of Ax=λx such an x is called an eigenvector corresponding to λ1
Eigenvector
An eigenvector of an n*n matrix A is a nonzero vector x such that Ax = λx for some scalar λ.
Difference equation
The recursively defined vector valued sequence
xk+1 = Axk
where A is an n*n matrix is called the difference equation
this can be rewritten to
xk+1 = A^k+1(x0)
if x0 is an eigenvector of A with associated eigenvalue λ this becomes
xk+1 = λ^k+1(x0)
If v1...vr are eigenvectors that correspond to distinct eigenvalues λ1 .... λr of an n * n matrix A then the set {v1 .... vr} is linearly independent
The eigenvalues of a triangular matrix are the entries on its main diagonal
Chapter 4
4.6 Change of Basis
Theorem !5
let B ={b1 ... b2} and c ={c1 ... c2} be the bases of a vector space v then there is a unique n * n matrix such that
[x]c = pc<-b[x]b
The columsn of pc<-b are the c-coordinate vectors of the vector in the basis b that is
pc<-b = [[b1]c [b2]c ..... [bn]c]
4.5 The Dimension of a Vector Subspace
Let A be an n*n matrix. Then the following statements are each equivalent to the statement that A is an invertible matrix
M The columns of A form a basis of R^n.
n. Col A + R6n
o. rank A = n
p. nullity A = 0
q. Nul A ={0}
infinite/finite
If a vector space v is panned by a finite set, then v is said to be finite-dimensional and the dimensions of V written as dim V, is the number of vectors in a basis for V. The dimensions of the zero vector space {0} is defined to be zero. if V is not spanned by a finite set, then V is said to be infinite-dimensional
rank/nullity
The rank of an m*n matrix A is the dimension of the column space and nullity of A is the dimension of the null space
Theorem 14
The Rank Theorem
The dimensions of the column space and the null space of an m*n matrix A satisfy the equation
rank A + nullity A = Number of columns in A
Theorem 13
The basis Therorem
let V be a p-dimensional vector space, p>+ 1 any linearly independent set of exactly p elements in v is automatically a basis for v any set of exactly p element that spans v is automatically a basis for v.
Theorem 12
Ltt H be a subspace of a finite dimensional vector space v. any linearly independent set in H can be expanded, if necessary, to a basis for H. Also H is finite-dimensional and
Dim H <= dim V
If a vector Space V has a basis of n vectors, then every basis of V must consist of exactly n vectors
If a vector space v has a basis B= {b1 .... bn} then an set in v containing more than n vectors must be linearly dependent
4.4 Coordinate Systems
B coordinates of x
Suppose B = {b1 ... bn} is a basis for a vector space v and x is in V. The coordinates of x relative to the basis B( or the B-coordinates of x) are the weights c1..cn such that x=c1b1+...+cnbn
Let B = {b1 ... bn} be a basis for a vector space V. Then the coordinate mapping x->[x]B is one to one linear transformation from v Onto R^N
Theorem 8
Unqiue Representation Theorem
Let B ={b1 ... bn} be a basis for a vector space v. then for each x in v there exist a unique set of scalars c1...cn such that
x = c1b1+...+cnbn
4.3 Linearly Independent Sets and Bases
Basis for H
Le t H be a subspace of a vector space v. A set of vectors B in V is a basis for H if
1.B is linearly independent se
2.The subspace spanned by b coincides with H that is
H= Span B
Indexed set dependent/independent
linearly dependent if there is a nontrivial solution to
c1v1+c2v2+...+cpvp = 0
Linearly independent if the vector
c1v1+c2v2+...+cpvp = 0
has only the trivial solution c1=0...cp=0
If two matrices A and B are row equivalent then thier row spaces are the same If b is in echelon form the nonzero rows of b for a basis for the row space of A as well as for that of B
The pivot columns of a matrix A form a basis for col A
The spanning set Theorem
let s = {v1 ... vp} be a set in a vector space v and let H = span {v1 ... vp}
a.If one of the vectors in s-say vk is a linear combination of the remaining vectors in s the the set formed S by removing vk still spans H
b. If H=/= {0} some subset of s is a basis for H
An indexed set {v1 ... vp} of two or more vectors with v1 =/= 0 is linearly dependent if and only if some vj ( with j >1) is a linear combination of the proceeding vectors v1...vj-1
4.2 Null, Column, Row Spaces and Linear Transformations
A linear transformation t from a vector space v into a vector space w is a rule that assign each vector x in v a unique vector t(x) in W such that
1.T(u+v)=T(u)+T(v) for all u, v in V
2.T(cu) = cT(u) for all u in V and all scalars C
contrast between Nul A and Col A
Nul A
1.Nul A is a subspace of R^n
2.Nul A is implicityly defined
3.it takes time to find vectors in nul A
4.There is no obvious relation between nul A and the entries in A
5.a typical vector v in nul a has the property that Av= 0
6.given a specific vector v it is easy to tell if v is in nul a just compute Avv
7.Nul A ={0} if and only if the equation Ax = 0 has only raised the trivial solution
8.Nul A ={0} if an only if the linear transformation x -> Ax is one to one
Col A
1. Col A is a subspace of R^m
2. Col A is explictly defined
3.easy to find col A
4.No obvious relation between Col A and the entries in A
5.Typical vector is consistent
6.Row operations are required
7.Col A =R^m if and only if the equation Ax=b has a solution for every b in R^m
8.Col A = R^m if and only if the linear trans x-. Ax maps R^n onto R^m
Row Space
If A is an m*n matrix for each row of A has n entries and thus can be identified with a vector R^n. the set of all linear combinations of the row vectors is called the row space of A and is denoted by Row A. Each row has n entries so Row A is a subspace of R^n. Since the rows of A are identified with the columns ofA^t we could also write Col A^t in place of Row A.
Column space
The column space of an m*n matrix A written as col A is set of all linear combinations of the columns of A if A = [a1 .. an] then
col A = Span {a1 . . . an}
Explicit Description of Nul A
We say that Nul A is defined implicate because it is defined by a condition that must be checked. No explicit list or description of elements in Nul A is given. However solving the equation Ax=b amounts to producing an explicate description.
null space
The null space of an m * n matrix A written as Nul A, is the set of all solutions o fthe homogenous equation Ax=0 in set notation
Nul = {x:x is in R^n and Ax=0}
The column space of an m* n matrix A is a subspace of R^m
The null space of an m*n matrix A is a subspace of R^n equivalently , the set of all solutions to a system Ax=0 of m homogenous linear equations in n unknowns is a subspace of R^n
4.1 Vector Space and Subspace
Subspaces
A subspace of a vector space v is a subset H of V that has three properties
a. The zero vector of V is in H
b. H is closed under vector addition. That is, for each u and v in H the sum u + v is in H
c. H is closed under multiplication by scalars. That is, for each u
Vector Space
A vector space is a nonempty set v of objects called vectors, on which are defined two operations addition and multiplication by scalars subject to the ten axioms listed below the axioms must hold for all vectors u, v, and w in v and for all scalars c and d
1.The sum, of u and v denoted by u + v is in V
2. u + v = v+ u
3.(u + v) + w = u + ( v + w )
4.There is a zero vector 0 in v such that u + 0 = u
5.For each u in v there is a vector -u in v such that u + (-u)=0
6.The scalar multiple of u by c denoted by cu is in v
7.c(u+v) = cu +cv
8.(c +d)u = cu + du
9.c(du) = (cd)u
10.lu = u
if v1 . . . . vp are in a vector space v, then span {v1 . . . . vp}
is a subspace of v
Chapter 3
3.3 Cramer's rule, Volume,
and linear Transformation
Theorem 10
2*2 [area of t(s)} = |det A|* {area of s}
3*3 [volumeof t(s)} = |det A|* {volumeof s}
Theorem 9
If A is a 2*2 matrix the area of the parallelogram determined by the columns of A is |detA|. If A is a 3*3 matrix the volume of the parallelpiped determined by the columns of A is |det A|
Theorem 8
Let A be an invertible n*n matrix then
A^-1 = 1/detA * adjA
Theorem 7
Let A be an invertible n * n matrix for any b R^n the unique solution x of Ax = b has entries given by
xi= detAi9b)/detA
3.2 : Properties of Determinants
Theorem 3
Let A be square matrix
a) if a multiple of one row of A is added to another row to produce a matrix B the det B = det A
B) if two rows of A are interchanged to produce B the det B = - Det A
C) If one row of A is multiplied by K to producde B, the det B = k Det A.
Theorem 6
If A and B are n * n matrices then det Ab= (detA)(Det B)
Theorem 5
If A is an n*n matrix the det A^t = det A
Theorem 4
A square matrix A is invertible if and only if det A =/= 0
3.1: intro to Determinants
Theorem 2
If A is a triangular matrix, then det A is the product of the entries on the main diagonal of A
Theorem 1
det A = ai1ci1 + ai2ci2 .... aincin
the cofactor expansion down the jth column is
det A = aijcj1 + aj2cj2 .... anjcnj
Chapter 2
2.9 Dimension and Rank
IMT Continued
IMT
m. The columns of A form a basis of R^n
n. Col A = R^n
o. rank A = n
p. dimNul A = 0
q.Nul A = {0}
Theorem 15
Theorem 15
Let H= be a p- dimenison subspace of R^n any linearly independent set of exactly p elements in H is automatically a basis for H also any set of p elements of H that spans H is automatically a basis for H
Theorem 14
Theorem 14
If a matrix A has n columns then rank A + dim Nul A = n
2.8 Subspaces of Rn
Theorem 13
Theorem 13
The pivot columns of a matrix A form a basis for the column space of A
Basis
Basis
a linearly independent set in H spans H
Null Space
Null Space
The null space of a matrix A is the set Nul A of all solutions of the homogenous equation Ax=0
Theorem 12
The null space of an m8n matrix A is subspace of R^N equivalently the set of all solution of a system Ax = 0 homogenous linear equations in n unkowns is a subspace
2.5: Matrix Factorization
Factorization
Factorization
an equation that expresses A as a product of two or more matrices
Algorithm For an lu factorization
Algorithm For an lu factorization
- reduce A to an echelon form U by a sequence of row replacement operations if possible
- Place entries in L such that the same sequence of row operations reduces L to l
2.4: Partitioned Matrices
Theorem 10
Theorem 10
if a is m*n and b is n* p then
AB = col1(a) col2(A) ....[row1(b) row2(b)
= col(A)tow1(b)......
2.3: Characterization of Invertible
Matrices
Theorem
let t: r^n ->r^n be a linear transformation and let A be the standard matrix for T then t is invertible iff A is an invertible matrix
Invertible Matrix Theorem
Invertible Matrix Theorem
a. is an invertible matrix.
b. A is a row equivalent to the n x n identify matrix.
c. A has n pivot positions.
d. The equation Ax = 0 has only the trivial solution.
e. The columns of A form a linearly independent set.
f. The linear transformation x -> Ax is one-to-one
g. The equation Ax = b has at least one solution for each b in R^n.
h. The columns of A span R^n.
i. The linear transformation x -> Ax maps R^n onto R^n.
j. There is an n x n matrix C such as CA = I.
k. There is an n x n matrix D such that AD = I.
l. A^T is an invertible matrix.
2.2: Inverse of a Matrix
Theorem 7
an n*n matrix A is invertible iff if a is row equivalent to in and in this case any sequence of elementary row operation that reduce a to in also transforms in into a^-1
Theorem 7
a) (a^-1)^-1 =A
b) (AB)^-1 =b^-1A^-1
c) A^t-1=A^-1^t
Theorem 5
Theorem 5
If A is an invertible n * n matrix then for each b in R6n the equation Ax=b has the uniques solution x=A^-1b
Theorem 4
Theorem 4
let [a b]
[c d]
if ad-bc =/= 0 then A is invertible and a^-1 = 1/ad-bc[d -b]
[-c a]
if ad-bc = 0 then A is not invertible
2.1: Matrix Operations
Sum and scalar multiples
Sum and scalar multiples
two m by n matrices A and B are said to be equal written as A=B
if r is a scalar and A is a matrix then the scalar multiple rA is the matrix whose columns are r times the corresponding columns in A
If A is an m*n matrix and if B is an n*p matrix with columns b1 ... bp then the product AB is the m * p matrix whose columns are ab1 ... abp
ab=A[b1 b2 ...bp]=[ab1.. ab2....abp]
Powers of a matrix
Powers of a matrix
if A is n*n and if k is a postive integer then A^k denotes the product of K copies of A:
A^k=A....A
Transpose
Transpose
given m * n matrix A the transpose is the n * M denoted by A^t
Theorem 3
Theorem 3
let A and B denote matrices whose size are appropriate for the following sums and products
A. (At)t = A
B. (A + B)t = At + Bt
C. (rA)t = eAt
D. (AB)t = BtAt
Theorem 2
Theorem 2
let A be an m * n matrix and let b and c have sizes which the indicated sums and products are defined
A. A(BC) = (AB)C
B. A(B+ C) = AB + AC
C. (B + C)A = BA + CA
D. r(AB) = (rA)B = A(rB)
E. ImA = A = AIn
Theorem 1
let A b and c be matrices of the same size and let r and s be scalars
A. A + B = B + A
B. (A + B) + C = A + (B + C)
C. A + 0 = A
D. r(A + B) = rA + rB
E. (r + s)A = rA + sA
F. r(sA) = (rs)A
Chapter 1
1.9 Matrix Of Linear Transformations
Theorem 12
Theorem 12
let T: r^n -> r^m be a linear transformation and let A be the standard matrix for t then
a} T maps R^n onto r^m if and only if the columns of a span r^m
b) t is one to one if and only if the columns of A are linearly independent.
Theorem 11
Theorem 11
let T: r^n -> r^m be a linear transformation the T is one to one if and only if the equation t(x) = 0 has only the trivial solution
Onto
Onto
a mapping t: r^n -. r^m is onto if each b in r^m is the image of a t least one x in R^n
One-to-One
One-to-One-
a mapping t: r^n -. r^m is one to one if each b in r^m is the image of at most one x in r^n
Matrix Transformation
Matrix Transformation
Describes how mapping is implemented
Standard Matrix for linear
transformation
Standard Matrix for linear transformation
A = [t9e1)...t(en)]
1.8: Intro to Linear Transformations
Linear Transformation
Linear Transformation
T is linear if
i) t(u+v) = T(u) + T(v) for all u v in the domain of T;
ii) T9cu) =cT(u) for all scalars c and all u in the domain of T0
Transformation
Transformation
function or mapping t from r^n to r^m is a rule that assigns each vector x in r^n a vector t(x) in R^m
Range
Range
the set of all images t(x) is called the range of T.
The range of t is the set of all linear combinations of the columns of A because each image t(x) is of the form Ax
Image
Image
the vector t(x) in R^M is called the image of x
Codomain
Codomain
the set R^m is called the codomain of t.
the codomain of T is R^m when each column of A has m entries.
Domain
Domain
the set R^n is called the domain of t.
the domain of t is r^n when a has n columns.
1.7 Linear Independence
Linearly Dependent
Linearly Dependent
the set v1... vp is linerly dependent if there exist weights c1....cp not all zeros such that
c1v1+c2v2+...cpvp=0
(called linear dependence relation)
Theorem 7
Theorem 7
an indexed set S = {v1.. vp} of two or more vectors is linearly dependent if and only if at least one of the vectors in s is a linear combination of the others in fact if s is linearly dependent and v1 =/= 0 then some vj (with j >1) is linear combination of the proceeding vectors v1.... vj-1
Theorem 8
Theorem 8
If a set contains more vectors than there are entries in each vector then the set is linearly dependent.
Theorem 9
Theorem 9
If a set S = [v1 ... vp] in R^n contains the zero vector, then the set is linearly dependent
Linearly Dependent Sets
Set of two Vectors
Set of two Vectors
if t
Linearly Independent
Linearly independent
indexed set of vectors v1...vp is linearly independent if x1v1+x2v2+ ... xpvp = 0 has only the trivial solution
columns of a matrix A are linearly independent if and only if the equation Ax=0 has only trivial solutions.
a set containing one vector v is linearly independent iff v is not the zero vector
1.6: Applications of Linear System
Equilibrium prices
Equilibrium prices
a number that exist that income balances expenses
1.5: Solutions Sets of linear Systems
Trivial and non Trivial Solution
Trivial solution
x=0
Non-Trivial solution
nonzero vector x that satisfies Ax= 0
Homogeneous
Homogeneous
System of linear equation that can be written Ax=0 where A is an m*n matrix and 0 is a zero vector. always one solution x=0
Theorem 6
Theorem 6
suppose the equation Ax= b is consistent for some given b, and let p be a solution. then the solution se of Ax=b is the set of all vectors of the form w= p + vh where vh is any solution of the monogenous equation Ax=0
1.4: Matrix equation Ax=b
Row- vector Rule for Computing ax
Row- vector Rule for Computing ax
If the product ax is defined then the ith entry in Ax is the sum of the products corresponding entries from row i of A and from vector x.
Finding B
Finding B
If A is an mxn matrix with columns a1 … an and if b is in r^M the matrix equation
Ax=b
Has the same solution set as the vector equation
X1a1 + x2a2 + …. + xnan =b
Which in turn has the same solution set as the system of linear equations whose augment matrix is
[a1 a2 …. An b]
This leads to the equation ax = b has a solution if and only if b is a linear combination of columns of A
Product of Ax
Product of Ax
If a in an m xn matrix with columns a1….an and if x is r^n then the product of A and x is denoted by Ax, is the linear combination of the columns of A using the corresponding entries in x a weights
Ex
Ax= {a1, a2 …… an} [x1] = x1a1 + x2a2 + …… +xnan
[xn]
1.3: Vector Equations
Span
Span
if V1....vp in r^n, then the set of all linear combinations of v1... vp is denoted by span{v1...vp} and is called the subset of R^n spanned ( or generated) by v1...vp. That is, span [v1...vp] is the collection of all vectors that can be written in the form
c1v1 + c2v2+...+cpVp
with c1 ... cp scalars
Linear Combinations
Linear Combination
Given vectors v1, v2 ...,vp in r^n and given the scalars c1, c2, ... ,cp the vector y defined by
y=c1v1+c2v2+vpvp
Algebraic Properties of R^n
Algebraic Properties of R^n
i) u + v = v+ u commentative property
ii) (u+v) + w = u + (v + w) associative property
iii) u + 0 = 0 + u = u zero property
iV) u + (-u)= -u+u=0 inverse property
V) c(u+v)=cu+cv distributive property
Vi) (c+d)u = cu + du distributive property
Vii) c(du)=(cd)u associative property of the multiplication
viii) 1u = u identity property
Vectors
Vectors
A matrix with only one column is called a column vector/ vector.
ex [ 1 ] [ 1 ]
[ 2 ] [ 3 ]
Two vectors are equal iff thier entries are equal
ex
[ 2 ] [ 2 ]
[ 5 ] [ 5 ]
Addition
Addition
given two vectors u and v their sum is the vector u + v by adding entries of u and v
ex
[ v1 ] [ u1 ] = [ v1+ u1 ]
[ v2 ] [ u2 ] = [ v2+ u2 ]
Parallelogram Rule for Addition
Parallelogram Rule for Addition
if u and v in r^2 are represented as points in the plane then u + v corresponds to the fourth vertex of the parallelogram whose other vertices are u, 0 and v
Multiplication
Multiplication
given vector u and a real number c the scalar multiple of u by c is the vector cu obtained by multiplying each entry in u by c
ex
c[ u ] [ r1 ] = [ cr1 ]
[ r2 ] = [ cr2 ]
Vector Equation
Vector Equation
x1a1+x2a2+...xnan=b
ex
[ 3 ] [ 1] [ 4 ]
x1[ 2 ] + x2 [-4 ] = [ 1 ]
[ 1 ] [-3 ] [ 3 ]
1.1: Systems of Linear Equations
Solution
Solution- a list s1, s2,... sn of numbers that make each equation a true statement
Systems of Linear equations
System of linear equations
a collection of one or more linear equations involving the same variables. 3 cases for solutions consistent system independent equations, inconsistent system independent equations, consistent system dependent equations.
consistent system dependent equations
consistent system dependent equations
System of linear equations have infinite number of solutions. Graph shows line on top of each other.
inconsistent system independent equations
inconsistent system independent equations
System of Linear equations has no solution. Graph is parallel lines.
consistent system independent equations
consistent system independent equations-
System of linear equations has one solution. has a graph that intersects in a single point.
Matrix Notation
Matrix Notation
two types coefficient matrix and augmented matrix. augmented matrix includes what the system of equations are equal to while coefficient does not.
Row Operations
Row operations
Used to solve system of equations
Three operations
- Interchange any 2 rows
- replace a row by multiplication (non-zero of that row)
- replace a row by the sum of that row and a constant nonzero multiple of another
1.2: Row Reduction and Echelon Forms
Pivot
Pivot Position
position in a matrix A is located in A that corresponds to a leading 1 in REF. in addition to a nonzero number needed to create zero by row operations
Pivot Column
a column that contains a pivot point.
Echelon Form
Echelon Form Requirements
- All nonzero rows are above any rows of all zeros
- Each leading entry of a row is in a column to the right of the leading entry of the row above it.
- All entries in a column below a leading entry are zero
Ex.
key - * any number @- leading entry
[ @ * * * ]
[ 0 @ * * ]
[ 0 0 @ * ]
[ @ * * *]
[ 0 0 @ *]
[ 0 0 0 0 ]
[ @ * * * ]
[ 0 @ * * ]
[ 0 0 0 * ]
Reduced row Echelon form
Reduced Echelon Form requirements
1-3. all previous steps form Echelon Form
4. The leading entry in each nonzero row is 1
5. Each leading 1 is the only nonzero entry in its column
Ex
key - * any number
[ 1 0 0 * ]
[ 0 1 0 * ]
[ 0 0 1 * ]
[ 1 0 * * ]
[ 0 1 * * ]
[ 0 0 0 0 ]
[ 1 * 0 * ]
[ 0 0 1 * ]
[ 0 0 0 * ]
Theorem 1
Theorem 1
Each matrix is row equivalent to one and only one reduced row echelon matrix.