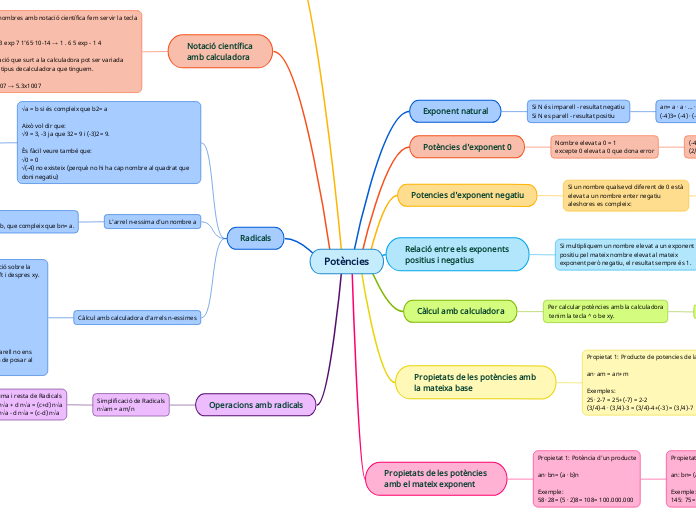
Potències
Operacions amb radicals
Simplificació de Radicals
n√am = am/n
Suma i resta de Radicals
c n√a + d n√a = (c+d) n√a
c n√a - d n√a = (c-d) n√a
Multiplicació i divisió de Radicals
n√am · n√ap= n√(am · ap)
n√am : n√ap= n√(am : ap)
Radicals
Càlcul amb calculadora d'arrels n-essimes
Farem servir la tecla x1/y , trobem aquesta funció sobre la tecla xy i per que actui hem de pitjar primer shift i despres xy.
Exemple:
Si volem calcular 5
√-243 → 5 shift xy
- 2 4 3 = i obtindrem -3.
Atenció: A la calculadora, els radicals d’índex parell no ens donaran les dues arrels però nosaltres les hem de posar al resultat.
Exemple:
Si volem calcular 5√-243 → 5 shift xy- 2 4 3 = i obtindrem -3.
Atenció: A la calculadora, els radicals d’índex parell no ens donaran les dues arrels però nosaltres les hem de posar al resultat.
L’arrel n-essima d’un nombre a
s’escriu n√a
és un nombre b, que compleix que bn= a.
Les parts d’un radical són les següents:
Radical
Index
Radicand
Arrel
4√16 = 2, -2, ja que 24= 16 i (-2)4= 16
6√-256 = no existeix, ja que cap nombre elevat a exponent parell dona negatiu
5√243 = 3, ja que 35= 243 (no -3, ja que (-3)5= -243)
7√-1 = -1, ja que (-1)7= -1
Hi ha diferències quan l’index és parell o senar i quan el radicand és positiu o negatiu.
a>0 n imparell=1arrel positiva/n parell=1arrel positiva negativa.
a=0 n parell o imparell=1arrel el 0
a<0 n imparell=1arrel negtiva/n parell= no té arrels reals
√a = b si és compleix que b2= a
Això vol dir que:
√9 = 3, -3 ja que 32= 9 i (-3)2= 9.
Ès fàcil veure també que:
√0 = 0
√(-4) no existeix (perquè no hi ha cap nombre al quadrat que doni negatiu)
∛a = b si és compleix que b3= a
A partir d’aquesta definició és fàcil veure que:
∛64 = 4, ja que 43= 64 (però no -4, ja que (-4)3= -64...)
∛-27 = -3, ja que (-3)3= -27
∛0 = 0, ja que 03= 0
L’arrel quadrada= nombre positiu= dues solucions, una negativa i una positiva.
L’arrel cúbica= nombre positiu=1 solució positiva.
L’arrel quadrada= nombre negatiu no existeix.
L’arrel cúbica= nombre negatiu sempre= nombre negatiu.
Notació científica
amb calculadora
Per escriure nombres amb notació científica fem servir la tecla exp.
Exemple:
5’3·107→ 5 . 3 exp 7 1’65·10-14 → 1 . 6 5 exp - 1 4
La representació que surt a la calculadora pot ser variada depenent del tipus decalculadora que tinguem.
Exemple:
5’3·107→ 5.307 → 5.3x1007
Exemple:
7’48·105+ 6’43·105→ 7 . 4 8 exp 5 + 6 . 4 3 exp 5 → 1.39105 → 1’391·105
S’ha de tenir cura en com escriure la solució, no serà valida solucions com les que dona la calculadora, el resultat s’ha d’escriure amb notació científica correcta.
Notació científica
Trobar una manera d’anotar aquestes
quantitats sense haver de posar tants zeros.
m · 10n
3’4 · 106
PASSAR DE NOTACIÓ CIENTÍFICA A NOTACIÓ NORMAL
Dos cassos:
CAS 1: La potència de 10 es positiva
Desplacem la coma a la dreta tants llocs com ens indiqui l’exponent.
Exemple:
3’546 · 105= 354600’ = 354600
CAS 2: La potència de 10 és negativa
Desplacem la coma a l’esquerra tants llocs com ens indiqui l’exponent.
Exemple:
2’3 · 10-4 = ’00023 = 0’00023
Propietats de les potències
amb el mateix exponent
Propietat 1: Potència d’un producte
an· bn= (a · b)n
Exemple:
58· 28= (5 · 2)8= 108= 100.000.000
Propietat 2: Potència d’un quocient
an: bn= (a : b)n
Exemple:
145: 75= (14 : 7)5= 25= 32
Propietats de les potències amb
la mateixa base
Propietat 1: Producte de potencies de la mateixa base
an· am = an+m
Exemples:
25· 2-7 = 25+(-7) = 2-2
(3/4)-4 · (3/4)-3 = (3/4)-4+(-3) = (3/4)-7
Propietat 2: Quocient de potencies de la mateixa base
an: am = an-m
Exemples:
25: 2-7 = 25-(-7) = 212
(3/4)-4 : (3/4)-3 = (3/4)-4-(-3) = (3/4)-1
Propietat 3: Potència d’una potència
(an)m = an·m
Exemple:
[(-3’14)-3]-5 = (-3’14)(-3)·(-5) = (-3’14)15
Molt importants els parèntesi, no és la mateixa expressió
(43)2, que la mateixa sense parèntesi.
Càlcul amb calculadora
Per calcular potències amb la calculadora
tenim la tecla ^ o be xy.
45= 4 ^ 5 = 1024
Relació entre els exponents
positius i negatius
Si multipliquem un nombre elevat a un exponent
positiu pel mateix nombre elevat al mateix
exponent però negatiu, el resultat sempre és 1.
Π2· Π-2 = 9’8696044... · 0’10132118... = 1
Això vol dir que aquests nombres són inversos l’un de l’altre.
Potencies d'exponent negatiu
Si un nombre qualsevol diferent de 0 està
elevat a un nombre enter negatiu
aleshores es compleix:
a-n = 1/an
(-4)-3 = 1/(-4)3= 1/(-4) · 1/(-4) · 1/(-4) = - 1/64
Potències d'exponent 0
Nombre elevat a 0 = 1
excepte 0 elevat a 0 que dona error
(-4)0= 1
(2/5)0= 1
Exponent natural
Si N és imparell - resultat negatiu
Si N es parell - resultat positiu
an= a · a · ... · a (multiplicació n vegades)
(-4)3= (-4) · (-4) · (-4) = -64