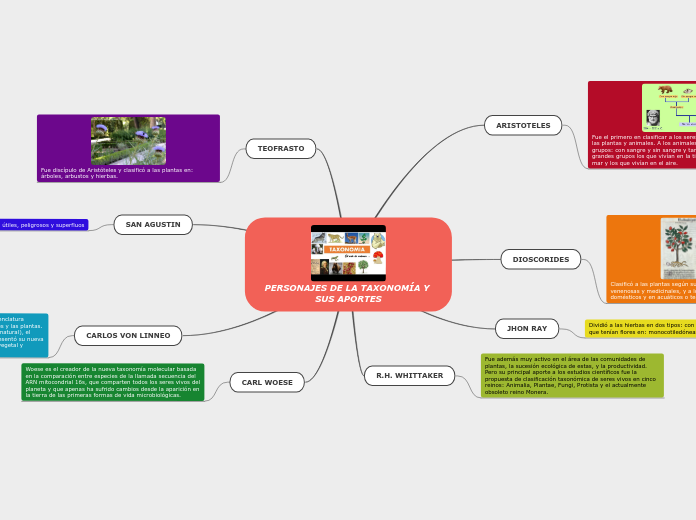
relaciones y funciones. dominio, contradominio y rango. clasificacion de funciones
Relizo: Medellin Aguilar Maria Fernanda, Mendez Espinosa Mariana Selene y Marchain Ruperto sergio Angel del cuarto C de hospedaje.
clasificacion de funciones
Funciones de probabilidad
En teoría de la probabilidad, una función de probabilidad (también denominada función de masa de probabilidad) es una función que asocia a cada punto de su espacio muestral X la probabilidad de que ésta lo asuma.
En concreto, si el espacio muestral, E de la variable aleatoria X consta de los puntos x1, x2, ..., xk, la función de probabilidad P asociada a X es
P(xi)=pi
donde pi es la probabilidad del suceso X = xi.
Funciones no elementales
Función hipergeométrica
Transformada de Laplace
Transformaciones lineales
Función de Ackermann
Función de Dirichlet
Función signo
Función mantisa
Función potencial: De la forma y = xa
Función parte entera
Función escalón unitario: En algunos países denominada Heaviside Step
Función módulo
Funciones Elementales
Funciones trascendentes
Funciones hiperbólicas
Se llaman funciones hiperbólicas al coseno hiperbólico (denotado cosh o ch), seno hyperbólico (senh o sh) y las funciones que se obtienen a partir de ellas, como la tangente (tanh o th), cotangente (coth), la secante (sech) y la cosecante (cosech) hiperbólicas:
Funciones trigonométricas
La trigonometría es la parte de las matemáticas que estudia los elementos de los triángulos, particularmente las relaciones entre sus lados y ángulos.
Subtema
Función logarítmica
Logaritmo natural o neperiano
La derivada de la función x \to x^n \ \mbox{ es } \ x \to n \cdot x^{n-1}, para todo n real. Dividiendo por n y mirando al revés la relación anterior, se puede afirmar que una primitiva de x \to x^m \ \mbox{ es } \ x \to \frac{1}{m+1} \cdot x^{m+1} (con m = n - 1). Este cálculo obviamente no es válido cuando m = - 1, porque no se podrá dividir por m + 1. Por tanto la función inversa: x \to x^{-1} = \frac 1 x es la única función "potencia" que no tiene una primitiva "potencia".
Sin embargo esta función es continua sobre ]0; +∞[ lo que implica que tiene forzosamente una primitiva en este intervalo, y también sobre ]-∞ ; 0[.
Acercamiento clásico
En primer lugar, sea la sucesión de término general x_n = (1+ \frac{1}{n})^n ; el límite de esta sucesión que es creciente y acotada superiormente existe. A ese límite se llama el número e, de suma importancia en matemáticas. Es un número irracional, no expresable mediante una fracción irreducible de números enteros, también es número trascendente, pues no puede ser raíz de una ecuación algebraica. Es un número real con valor aproximado: 2,718281328...
Función exponencial
La función exponencial es la recíproca de la función logaritmo natural.
Funciones algebraicas
Función raíz
Se llama función raíz enésima o función raíz de orden n a su función recíproca
Función racional
Las funciones racionales son funciones obtenidas al dividir una función polinomial por otra no idénticamente nula.
Están definidas en todos los números que no anulan el polinomio denominador, es decir, en todos los números reales menos una cantidad finita, que será igual al número de raíces reales del polinomio denominador. Una función racional está definida en todo R si el polinomio denominador no tiene raíces reales.
Función polinómica: Se llama función polinómica a toda función que se pueda expresar de la forma x → P(x) donde P es un polinomio en x, es decir, una suma finita de potencias de x multiplicadas por ciertos coeficientes.
funciones cúbicas
vienen dadas por un polinomio de tercer grado, ax3 + bx2 + cx + d.
funciones cuadráticas
vienen dadas por un polinomio de segundo grado, ax2+ bx + c.
funciones lineales
vienen dadas por un polinomio de primer grado, ax + b.
dominio, contradominio y rango
Rango o Contradominio
RANGO O CONTRADOMINIO: El conjunto de todos los valores resultantes de la variable dependiente “y”. Otros nombres para éste son: rango (muy empleado en cálculo),Son todos los valores que puede tomar
Rango o Contradominio: El conjunto de todos los valores resultantes de la variable dependiente “y”. Otros nombres para éste son: rango (muy empleado en cálculo),Son todos los valores que puede tomar Y
Ejemplos; Función con Dominio X y Codominio Y Para la función , en cambio, si bien su dominio es , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
Note que a cada elemento de X le corresponde un único elemento de Y.
dominio
Es el conjunto de valores para los que una determinada función matemática está definida. El dominio de es el conjunto de existencia de la misma, es decir, los elementos para los cuales la función está definida Dominio son todos los valores que puede tomar X.
Ejemplos; Función con Dominio X y Condominio Y Para la función, en cambio, si bien su dominio es, sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
Note que a cada elemento de X le corresponde un único elemento de Y.
En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota o bien . En se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
relaciones y funciones
todas las funciones son relaciones , pero no todas las relaciones son funciones.
toda ecuación es una Relación , pero no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.
En Matemáticas, dados dos conjuntos X e Y, una función o aplicación de X en Y es una correspondencia matemática denotada
que cumple con las siguientes dos condiciones:
Condición de existencia: Todos los elementos de X están relacionado con elementos de Y, es decir,
Condición de unicidad: Cada elemento de X esta relacionado con un único elemento de Y, es decir, si
Una función es un caso particular de relación y de correspondencia matemática. Cada relación o correspondencia de un elemento con un (y sólo un) se denota , en lugar de
funcion
Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Relación
Relación es la correspondencia de un primer conjunto, llamado Dominio , con un segundo conjunto, llamado Recorrido o Rango , de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.