da Ali Rizvi mancano 2 anni
139
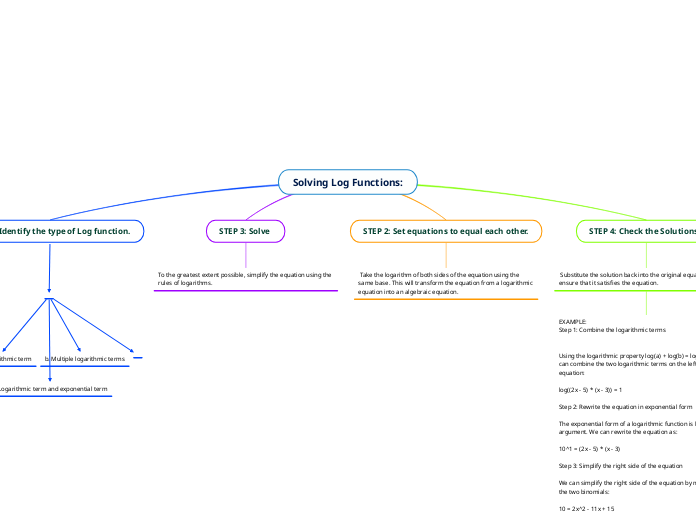
Solving Log Functions:
To solve logarithmic functions, one must first combine the logarithmic terms using properties of logarithms, such as the addition property. The next step involves rewriting the logarithmic equation in its exponential form, converting the equation into a more familiar algebraic format.