Сортировка

もっと見る

Психокоррекционные программы

Малышева Анастасия Владимировнаにより

Что можно делать с информацией?

Ксения Кульгаеваにより

Хід уроку

Юлия Голозубоваにより

Педагогическая рефлексия (по видам рефлексии)

Ксения Ояにより

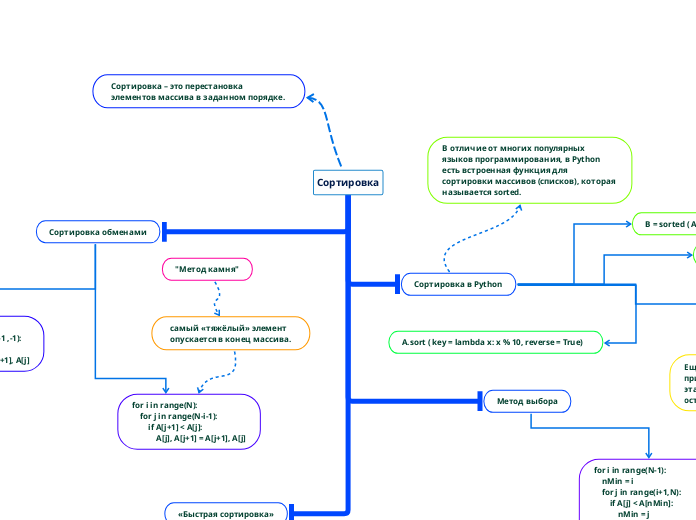
A.sort ( key = lambda x: x % 10, reverse = True)

B = sorted ( A, key = lambda x: x % 10 )

def lastDigit ( n ): return n % 10 B = sorted ( A, key = lastDigit )

B = sorted ( A, reverse = True )

B = sorted ( A )

В отличие от многих популярных языков программирования, в Python есть встроенная функция для сортировки массивов (списков), которая называется sorted.

Если длина массива не больше 1, то ответ – это сам массив, сортировать тут нечего (строка 1). Иначе выбираем в качестве разделителя («стержневого элемента», англ. pivot) X случайный элемент массива (строка 2), для этого используется функция choice (в переводе с англ. – выбор) из модуля random.. В строках 3-5 с помощью генераторов списков создаем три вспомогательных массива: в массив B1 войдут все элементы, меньшие X, в массив BX – все элементы, равные X, а в массив B2 – все элементы, большие X. Теперь остается отсортировать списки B1 и B2 (вызвав функцию qSort рекурсивно) и построить окончательный список-результат, который «складывается» из отсортированного списка B1, списка BX, и отсортированного списка B2.

Скорость работы быстрой сортировки зависит от того, насколько удачно выбирается вспомогательный элемент X. Самый лучший случай – когда на каждом этапе массив делится на две равные части. Худший случай – когда в одной части оказывается только один элемент, а в другой – все остальные. При этом глубина рекурсии достигает N, что может привести к переполнению стека (нехватке стековой памяти).

В середине XX века математики и программисты серьезно занимались разработкой более эффективных алгоритмов сортировки. Один из самых популярных «быстрых» алгоритмов, разработанный в 1960 году английским учёным Ч. Хоаром, так и называется – «быстрая сортировка»

Еще один популярный простой метод сортировки, при котором на каждом этапе выбирается минимальный элемент (из оставшихся) и ставится на свое место.

Еще один популярный простой метод сортировки, при котором на каждом

этапе выбирается минимальный элемент (из оставшихся) и ставится на свое место.



самый «тяжёлый» элемент опускается в конец массива.

"Метод камня"

"Метод пузырька"

сначала поднимается «наверх» (к началу массива) самый «лёгкий» (минимальный) элемент, затем следующий и т.д.

import random def qSort ( A ): if len(A) <= 1: return A X = random.choice(A) B1 = [ b for b in A if b < X ] BX = [ b for b in A if b == X ] B2 = [ b for b in A if b > X ] return qSort(B1)+BX+qSort(B2)

def qSort ( A, nStart, nEnd ): if nStart >= nEnd: return L = nStart; R = nEnd X = A[(L+R)//2] while L <= R: while A[L] < X: L += 1 while A[R] > X: R -= 1 if L <= R: A[L], A[R] = A[R], A[L] L += 1; R -= 1 qSort ( A, nStart, R ) qSort ( A, L, nEnd ) qSort ( A, 0, N-1 )

for i in range(N-1): nMin = i for j in range(i+1,N): if A[j] < A[nMin]: nMin = j if i!= nMin: A[i], A[nMin] = A[nMin], A[i]

Еще один популярный простой метод сортировки, при котором на каждом

этапе выбирается минимальный элемент (из оставшихся) и ставится на свое место.

for i in range(N): for j in range(N-i-1): if A[j+1] < A[j]: A[j], A[j+1] = A[j+1], A[j]

for i in range(N-1): for j in range(N-2, i-1 ,-1): if A[j+1] < A[j]: A[j], A[j+1] = A[j+1], A[j]

Сортировка – это перестановка элементов массива в заданном порядке.

Сортировка

«Быстрая сортировка»

Сортировка обменами

Метод выбора

Сортировка в Python