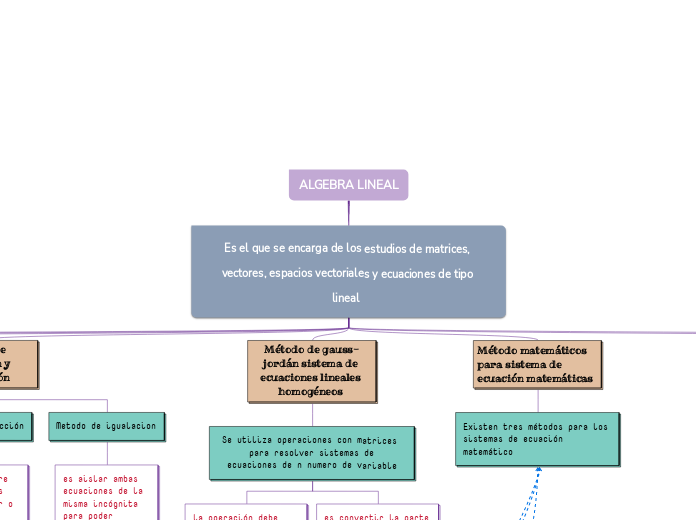
ALGEBRA LINEAL
Es el que se encarga de los estudios de matrices, vectores, espacios vectoriales y ecuaciones de tipo lineal
Aplicación de vectores
Vida cotidiana
Nuestros movimientos pueden ser representados por vectores, ya que se tiene una dirección, un sentido y una dimensión.
Añada su texto
Programación e informática
son empleados como contenedores de datos, con arreglos que contiene un valor determinado que servira para realizar o completar las instrucciones que ejecuta un programa
Matematicas
Es la materia en la que se hace un estudio u aplicacion bastante a menudo de los vectores,son en el estudio del álgebra lineal, las ecuaciones diferenciales, análisis matemático, cálculo
Vectores
Es un segmento de recta en el espacio que parte de un punto hacia otro que tiene dirección y sentido
Existen varios tipos de vectores
axiales o pseudovectores
son los que están ligados a efectos de giro. La dirección señala el eje de rotación del segmento
Colineales
sus líneas de acción se encuentran sobre una misma recta
coplanarios
son aquellos que están en un mismo plano
Equipolentes o iguales
vectores con igual módulo, dirección y sentido
Libres
Cuyo punto de aplicación es indeterminado y, por lo tanto, libre
Opuestos
se caracterizan por tener la misma dirección y magnitud, pero su sentido es opuesto
paralelos
Poseen un mismo sentido o contrario
vectores fijos
Se expresan un punto de origen además de un extremo, el cual está determinado en un punto fijo del espacio.
Unitarios
son aquellos cuyo módulo es igual a 1
Nulos
Son aquellos donde el origen, extremo coinciden y el modulo o magnitud es igual a 0
Concurrentes o angulares
Líneas de acción pasan por el mismo punto
Método matemáticos para sistema de ecuación matemáticas
Existen tres métodos para los sistemas de ecuación matemático
Método de gauss-jordán sistema de ecuaciones lineales homogéneos
Se utiliza operaciones con matrices para resolver sistemas de
ecuaciones de n numero de variable
es convertir la parte de la matriz donde se encuentra los coeficientes de las variables en una matriz identificada
la operación debe aplicarse a toda la fina o columna
Método de igualación y sustitución
Metodo de igualacion
es aislar ambas ecuaciones de la misma incógnita para poder igualar la expresión
Metodo de reducción
es operar entre las ecuaciones tal como sumar o restar ambas ecuaciones de modo que una de las incógnitas desaparezca
Metodo de sustitucion
consiste en despejar o aislar una de las incognitas sustituyendo la ecuacion con otra
Sistema de ecuación
Conjunto de dos o mas ecuaciones con varias incógnitas en la que se encuentra una solución
Incompatible
No tienen ninguna solución, es representada por dos rectas paralelas
Compatible determinado
Solo tiene una única solución, representado con dos rectas que se cortan en un punto.
Compatible indeterminado
Tiene muchas soluciones y la representación son dos rectas que coinciden
Inversa de una matriz
Es una herramienta importante en la resolución de sistemas de ecuaciones lineales puesto que cualquier sistema puede ser escrito en la forma A\vecx=\vecb
Propiedades de la matriz inversa
Si A^T denota la transpuesta de una matriz, entonces
(A^T)^-1=(A^-1)^T
Sea k un número real no cero, entonces
(k A)^-1=k^-1 A^-1
(A^-1)^-1=A
Sean A y B matrices invertibles del mismo orden, entonces el producto A B es invertible y además
(A B)^-1= B^-1A^-1
Matrices
Conjunto bidimensional de números o elementos dispuestos en filas y columnas, organizadas en forma rectangular.
Existen distintos tipos de matrices
Matriz es rectangular
No es cuadrada, tiene diferente numero de fila que de columna
Matriz es cuadrada
Cuanta con el mismo numero de filas que de columna
Mattriz columna
Solo conta de una columna
Matriz fila
Solo tiene una fila
Matriz nula
Tiene todos los elementos en cero