によって García Arellano Arath 3年前.
413
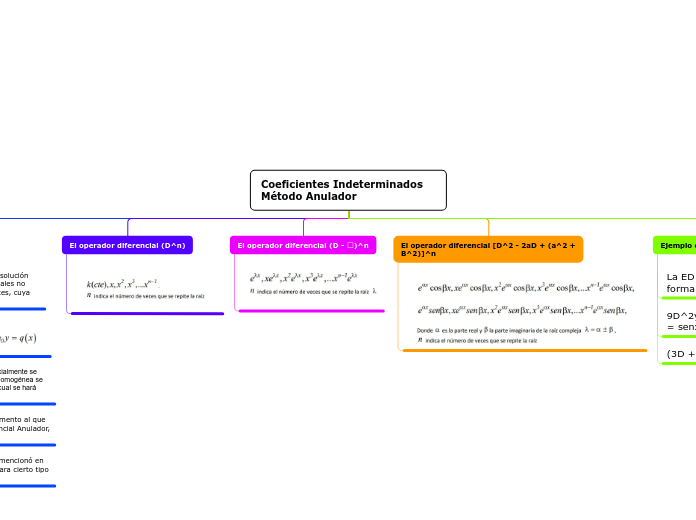
Coeficientes Indeterminados Método Anulador
El método de coeficientes indeterminados con operador anulador se utiliza para resolver ecuaciones diferenciales no homogéneas con coeficientes constantes. Este procedimiento busca encontrar una solución particular transformando la ecuación no homogénea en una homogénea a través de la anulación de la función q(