によって Carmen Mercedes CAYO CAMPOS 1年前.
147
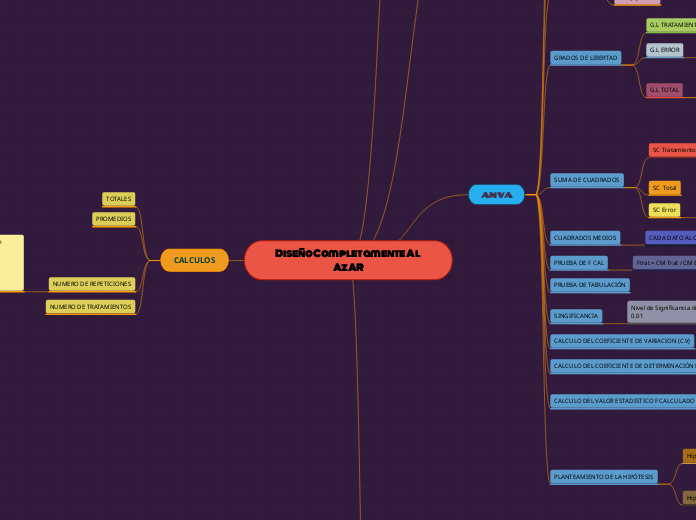
Diseño Completamente Al AzAR
El texto aborda la metodología para realizar pruebas de comparación de medias, incluyendo varios tipos de pruebas como las de Duncan, Tukey y Dunnet. Se describen los pasos a seguir, que comienzan con el ordenamiento de las medias y el planteamiento de hipótesis, seguido por el cálculo de errores estándar y valores críticos.