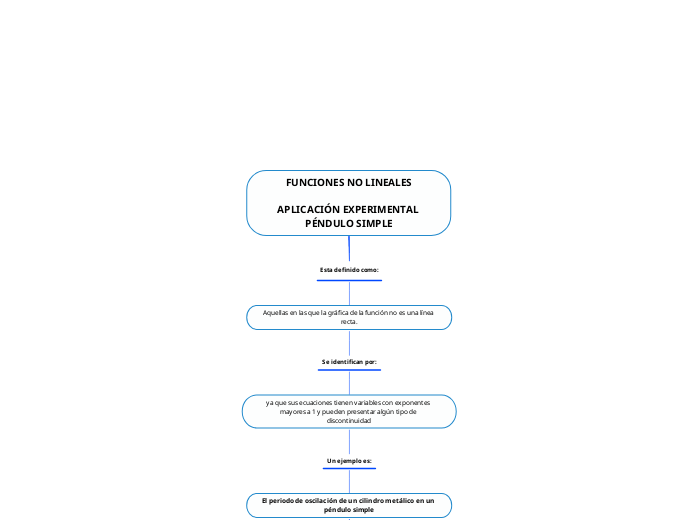
FUNCIONES NO LINEALES
APLICACIÓN EXPERIMENTAL PÉNDULO SIMPLE
Esta definido como:
Aquellas en las que la gráfica de la función no es una línea recta.
Se identifican por:
ya que sus ecuaciones tienen variables con exponentes mayores a 1 y pueden presentar algún tipo de discontinuidad
Un ejemplo es:
El periodo de oscilación de un cilindro metálico en un péndulo simple
Para este experimento se calcula:
medidas indirectas
el resultado de emplear una expresión matemática
Las magnitudes halladas va a ser:
La función de la regresión no lineal
Vd = k (Vi)ª
ecuación 3
La cual se le aplicara logaritmos naturales y sus respectivas propiedades
ln Vd = ln K + a ln Vi
ecuación 4
esta conformada por:
Vi
donde:
Vi -> L
L es La longitud del péndulo
a
usando la ecuación 7
K
se halla:
k = eᵇ
ecuación 5
b
es la ecuación 6
e
Es el número de Euler
X = Desplazamiento horizontal
ecuación 2
X̅ = El promedio o valor medio
ecuación 1
medidas directas
definidas como:
aquellas donde el instrumento de medición mide directamente la magnitud desconocida
La magnitud medida es:
El periodo que oscila el cilindro metálico
utilizando:
cronometro Pasco
El tiempo de oscilación depende de:
Longitud
La longitud del péndulo (L) la constituye la distancia en (m) desde el punto de
suspensión O hasta el centro de masa del objeto que oscila
La longitud del péndulo va a ser de:
0,80m
0,60 m
0,45 m
0,35 m
0,25 m
0,15 m
Amplitud
La amplitud de la oscilación (X) se define como el desplazamiento horizontal de la
masa con relación al punto de equilibrio o posición intermedia medido en (m)
La Amplitud de la oscilación va a ser: X
donde
X se halla de la ecuación 2 con θ = 5°
Masa
que es:
La masa es magnitud física que expresa la cantidad de materia de un cuerpo
para este experimento
La masa de un cilindro de cobre, aluminio o acero.