によって Angie Gordillo 6年前.
266
Mate
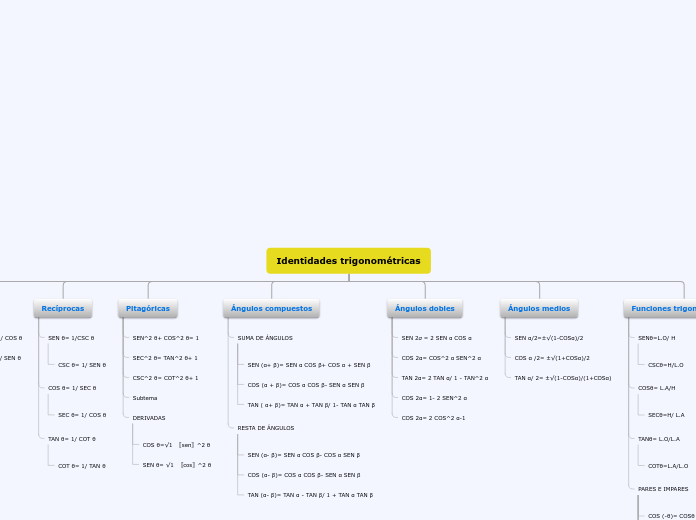
Las identidades trigonométricas son fundamentales en el estudio de las matemáticas y la física, proporcionando relaciones cruciales entre las funciones trigonométricas. Estas identidades incluyen fórmulas para ángulos dobles y medios, así como para ángulos compuestos, que permiten simplificar y resolver ecuaciones complejas.
開く
Identidades trigonométricas Funciones trigonométricas PARES E IMPARES SEN (-θ)= -SENθ CSC (-θ)= -CSCθ SEC (-θ)= SECθ COT (-θ)= -COTθ TAN (-θ)= -TANθ COS (-θ)= COSθ TANθ= L.O/L.A COTθ=L.A/L.O COSθ= L.A/H SECθ=H/ L.A SENθ=L.O/ H CSCθ=H/L.O Ángulos medios TAN α/ 2= ±√(1-COSα)/(1+COSα) COS α /2= ±√(1+COSα)/2 SEN α/2=±√(1-COSα)/2 Ángulos dobles COS 2α= 2 COS^2 α-1 COS 2α= 1- 2 SEN^2 α TAN 2α= 2 TAN α/ 1 - TAN^2 α COS 2α= COS^2 α SEN^2 α SEN 2α = 2 SEN α COS α Ángulos compuestos RESTA DE ÁNGULOS TAN (α- β)= TAN α - TAN β/ 1 + TAN α TAN β COS (α- β)= COS α COS β- SEN α SEN β SEN (α- β)= SEN α COS β- COS α SEN β SUMA DE ÁNGULOS TAN ( α+ β)= TAN α + TAN β/ 1- TAN α TAN β COS (α + β)= COS α COS β- SEN α SEN β SEN (α+ β)= SEN α COS β+ COS α + SEN β Pitagóricas DERIVADAS SEN θ= √1 〖cos〗^2 θ COS θ=√1 〖sen〗^2 θ Subtema CSC^2 θ= COT^2 θ+ 1 SEC^2 θ= TAN^2 θ+ 1 SEN^2 θ+ COS^2 θ= 1 Recíprocas TAN θ= 1/ COT θ COT θ= 1/ TAN θ COS θ= 1/ SEC θ SEC θ= 1/ COS θ SEN θ= 1/CSC θ CSC θ= 1/ SEN θ Cocientes COT θ= COS θ/ SEN θ TAN θ= SEN θ / COS θ