によって caterin garzon 4年前.
323
Organigrama
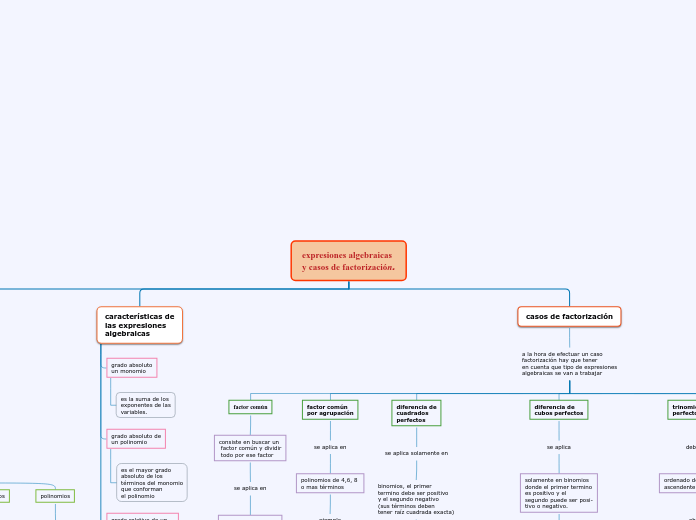
Las expresiones algebraicas combinan letras y números mediante operaciones aritméticas. Se clasifican en monomios, binomios, trinomios y polinomios, según el número de términos que las componen.
によって caterin garzon 4年前.
323

もっと見る
* El trinomio debe estar organizado en forma descendente. *El coeficiente principal (es decir, del primer término) debe ser positivo y diferente de uno. * el primer termino debe estar elevado al doble grado del exponente del segundo termino.
5p^2+13p-6 =(p+3)(5p-2)
* El trinomio debe estar organizado en forma descendente. * El coeficiente del primer término debe ser uno (1) *el primer termino debe estar elevado al doble del grado del exponente del primer termino
x^10-13b+30 =(x^5-10)(x^5-3)
debe estar
ordenado de forma ascendente o descendente
ehemplo
x2 − 6x + 9 = (x − 3)2
se aplica
solamente en binomios donde el primer termino es positivo y el segundo puede ser posi- tivo o negativo.
los coeficientes son números que tienen raíz cuadrada perfecta.
m^9+64a^6=(m^3+4a^2)((m^3 )^2-m^3 a^2+(4a^2 )^2) =(m^3+4a^2)(m^6-4a^2 m^3+16^4)
se aplica solamente en
binomios, el primer termino debe ser positivo y el segundo negativo (sus términos deben tener raíz cuadrada exacta)
x² – 9 = (x+3)(x-3)
polinomios de 4,6, 8 o mas términos
ax + ay + 4x + 4y =(ax + ay)+(4x + 4y) Agrupando términos = a(x + y) + 4(x + y)
consiste en buscar un factor común y dividir todo por ese factor
se aplica en
binomios, trinomios y polinomios de 4 términos o mas.
ejemplo
*10a-15b=5(2a-3b)
pueden ser expresadas por
polinomios
constan de 4 o mas terminos
trinomios
constan de 3 terminos
*-2a^2+x^3-3ax *4b+5a^3-2x
binomios
constan de 2 términos
*-3x+2b *4a^2 z-2x^2
moniomios
constan de solo 1 termino
ejemplos
*5x *-7ab
como
radicación
potenciación
division
multiplicacion
resta
suma