によって Alan Oportus 4年前.
370
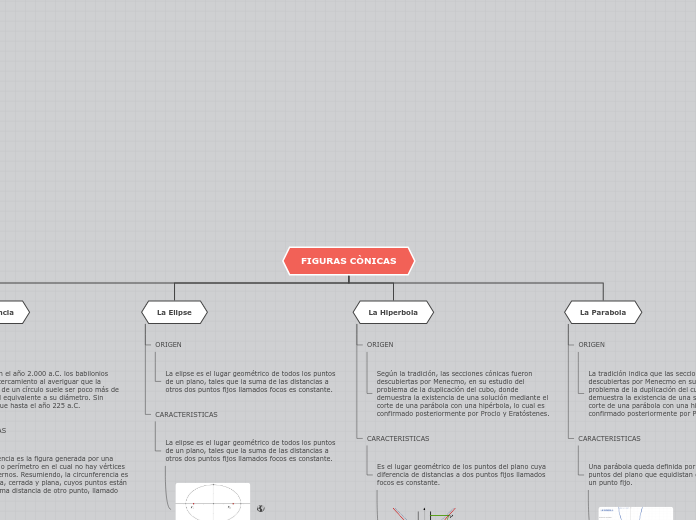
Organigrama arbol
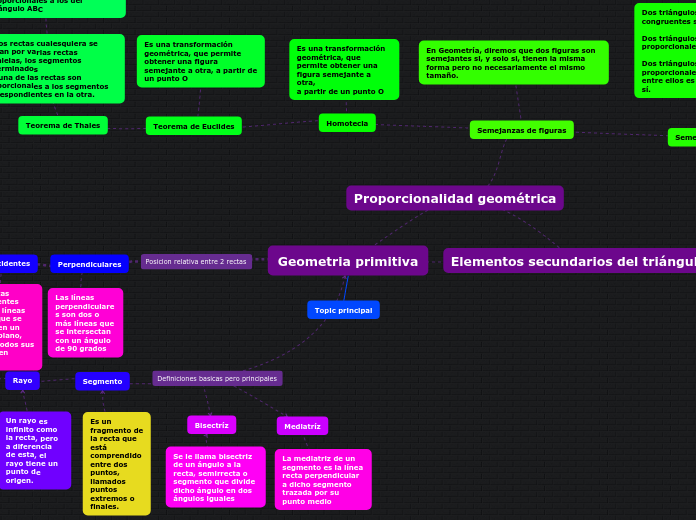
El texto trata sobre diversos conceptos geométricos relacionados con triángulos y rectas. Se menciona el incentro, que es el punto de intersección de las bisectrices de un triángulo y el centro de la circunferencia inscrita.