pensamiento matemático
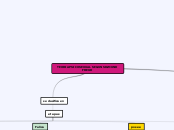
En el estudio de las matemáticas, uno de los conceptos fundamentales es el de función, que puede ser abordado desde diferentes perspectivas como los límites, la continuidad y la clasificación de funciones.
開く
Funciones, Modelos y Límites de una función. Clasificación de Funciones Funciones logarítmicas. Son las funciones f x x a ( ) = log donde
la base a > 0 y a ¹ 1. Son las funciones
inversas
de las funciones exponenciales. Funciones exponenciales. Son las funciones de la forma x f (x) = a ,
donde la base a es una constante positiva.
El dominio es  y la imagen es (0,¥) . Funciones racionales. Una función racional f es una
razón de dos polinomios. Función polinomial de grado. Función asociada a un polinomio. Función cúbica. Como su nombre lo indica,
la expresión analítica es un polinomio
de tercer grado. Posee la
forma f x = ax + bx + cx + d 3 2 ( ) a ¹ 0 Función Cuadrática. Es de la forma: f x = ax + bx + c 2 ( ) a ¹ 0 Función lineal. Se representa de la forma f (x) = mx + b ,
en donde m y b son constantes. Función de identidad. Como su nombre lo indica,
la imagen es igual al argumento.
Posee la forma: f (x) = x Función constante. Es aquella de la forma f (x) = k ,
donde k es una constante. Límites. Límites al infinito. Continuidad Continuidad en un punto.
Asintota Vertical. Asintota Horizontal. Límites especiales. Indeterminaciones teniendo en cuenta a que tiende X. Límites determinados e indeterminados. Función Dominio de una Función. serán las extensiones de la
ecuación implicada,
a menos que se indique otra cosa Representación de una Función Analítica. Gráfica. Sagital.