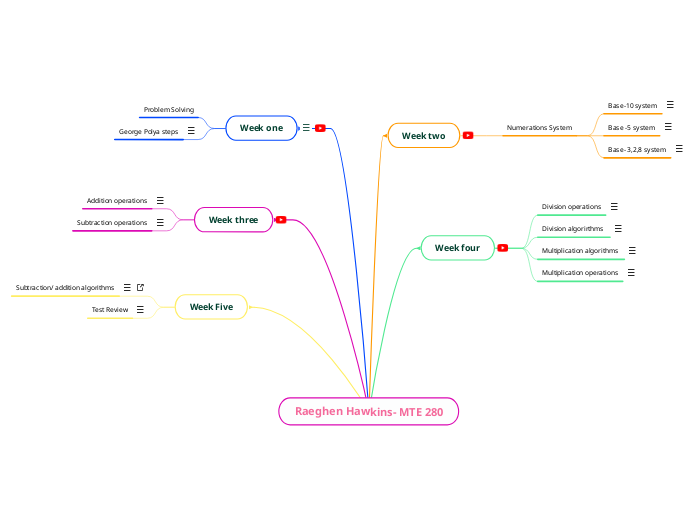
によって Raeghen Hawkins 1年前.
56
もっと見る
Test Review:
20 questions
Subtraction Algorithms:
1) American standard:
13
5 3 15
645
-279
-------
366
2) Europe/Mexican
14 15
645
-279 2 become a 3 and 7 becomes 8 so 4 and 5 become 14 and 15
-------
366
3) Reverse Indian
14 15
645
-279
-------
4
37
6
6
--------
366
4)Left-to-right
14 15
645
-279
------
400
300
70
60
6 =366
5) Expanded notation
130
500 30 15
645= 600-40-5
-279= 200-70-9
----------------------
366= 300+60+6
6) Integer subtraction
645
-279
-------
-4
-30 400-30-4
+400
--------
366
Addition Algorithms:
1) American Standard
1 1
478
+ 394
------
872
2) Partial Sums
4|7|8
+3|9|4
----------
|1|2
1|6|
7| |
-------------
872
3) partial sums with place value
4|7|8
+3|9|4
----------
|1|2
1|6|0
+ 7|0|0
-------------
872
4)Left-to-right
478
+394
---------
700
160
12
-------
872
5)Expanded notation
100 10
478= 400+70+8
+394= 300+90+4
-------------------------
872= 800+70+2
6)Lattice
478
+394
---------
0/ 1/ 1/
7/ 6/ 2
-----------
8/7/2
------->
Subtraction Operations
meaning: take away
7-3=4
7 is the minuend
3 is the subtrahend
4 is the difference
Addition meaning: Combine/join groups together
3+4=7
3 & 4 are the addends and 7 is the sum
4+0=4
-3+0=-3
The order in which I add the #'s don't matter
(2+3)+5=2+(3+5)
Problem solving:
1) understand- tell me what the problem says
2) plan- whatever strategy makes sense (trial and error/ work backwards)
3) Implement- do you plan test it out (make the problem simpler/find a patter/be patient don't give up)
4) look back and is it reasonable- explain how? (does it make sense/ what did you learn/ did you answer all the questions?/ could it be done differently)
Problem #1:
12 basketball teams in a league if each team plays each other once how many games take place?
Teams: T1, T2, T3, T4, T5, T6, T7, T8, T9, T10, T11, T12
# of games: 0 1 3 6 10 15 21 28 36 45 55 66
+1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11
The amount of games that would be played if each of the 12 teams played each other once time there would be 66 games played. I found this out by finding a pattern in a table for each team that was added the amount of games played would go up by 1 from the previous number.
Problem #2:
7 9 cent
X5 6 cent
---------
35 7+5+35=47
George Polya steps:
1) Understand - tell me what the problem says/ what are you asked to find
2)Plan- Devise a plan/trial and error/make a table/ try different ways
3)Implement- do your plan try it out/make the problem simpler/be patient/explain how?
4)Look back is it reasonable- does it make sense/ what did you learn/did you answer all questions?/ could it have been a different way?
Multiplication operations:
meaning: repeated addition
3x2=6
3 & 2 are the factors
6 is the product
3x2 could be 3 groups of 2
Group 1: has 2 cookies
Group 2: has 2 cookies
Group 3: has 2 cookies
2+2+2=6
Distribution property of multiplication:
3x7=3x(5+2)= (3x5)+(3x2)
(5+2) & (3x5) are partial products
3x7=3x(5+2) = (3x5) + (3+2)= 15+6= 21
= 3x(3+4)= 9+12=21
= 3x(6+1)= 3x6+ (3x1)= 19+2=21
Multiplication algorithms
1)American standard
1
23
X 14
--------
92
1
230
------
322
2) Expanded notation place v.explicit
23
x 14
--------
10
20+3
10+4
---------
100+90+2
200+30+0
-------------
300+20+2
---------------
322
3)Place value
23
x14
------
4x3=12 } 92
4x20-80 }
10x3=30 } 230 92 and 230 are partial products
10x20=200 }
----------------
322
4)Lattice (x)
23 X
/ 1/ 1
0 / 0/ 4
2/3/
------
0/1/
8/2/
3 2 2
------
322
Division algorithms:
158
3|-475
-3
-17
15
-25
24
---------
1
158
3|-475
-300
------
175
-150
------
25
-24
------
1
197 cookies and there are 16 in each box how many boxes will we need?
12
16|-197
-160 -----> 10 boxes
---------
37
-32 -----> 2 boxes
---------
5 10
+2
-------
12 boxes will be needed
Division Operations:
meaning: repeated subtraction (it is sharing between a certain # ex:2)
8/2: division sign
8: - is the division fraction bar
2
2|- 8: this is the vinculumn
2|-8= 4
4 is the quotient
2 is the divisor
8 is the dividend
Ex:
11/3
11-3=8
8-3=5
5-3=2
Base-3: (0,1,2)
Base-3 place values:
Ones:3^0
Threes: 3^1
Nines: 3^2
Twenty-sevens: 3^3
Base-8: (0,1,2,3,4,5,6,7)
Base-8 place values:
Ones: 8^0
Eights: 8^1
Sixty-fours: 8^2
Base-2: (0,1)
Base-2 place values:
Ones: 2^0
Twos: 2^1
Fours: 2^2
Eights: 2^3
sixteens: 2^4
Example:
A) 111_2= (1x2^2)+(1x2^1)+(1x2^0)
= 4+2+1
=7
B) 31.2_4= (3x4^1)+(1x4^0)+(2x 1/4)
= 12+1+2/4
=13 1/2
Expanded notation:
738= (7x10^2)+(3x10^1)+(8x10^0)
=(7x100)+(3x10)+(8x1)
= 700+ 30+ 8= 736
Base-5 #'s: 0,1,2,3,4,10,11,12,13,14,20 (0-4)
Base-5 palace values:
Ones: 5^0
Fives: 5^1
25's: 5^2
125's: 5^3
Base-5 conversion to Base-10
Example:
212_5= (2x5^2)+(1x5^1)+(2x5^0)
= (2x25)+5+2
= 50+5+2
= 57
Another example:
2304_5= (2x5^3)+(3x5^2)+(0x5^1)+(4x5^0)
= (2x125)+(3x25)+(0x5)+(4x1)
=250+75+0+4
=392
Base 10|Base5
1 | 1_5
2 | 2_5
3 | 3_5
4 | 4_5
5 | 10_5
6 | 11_5
7 | 12_5
8 | 13_5
9 | 14_5
10 | 20_5
11 | 21_5
12 | 22_5
There is no 5's in base-5 No(5,15,25,35,45,50)
goes from 144-200
Base 10 #'s- 0,1,2,3,4,5,6,7,8,9
10 is where the double digits come in they have 2 places values
in base 10 number get their value by where they sit
EX: 375
The 3=300 it is in the hundred place
The 7=70 it is in the tens place
The 5=5 it is in the ones place
there is also a thousands place
Ones place = a singular cube
tens place= a stick of ten cubes
hundreds= a flat square
thousands= a large cube
Expanded notation in base-10:
375+ 300+70+5
= (3x100) + (7x10) + (5x1)
= (3x10^2) + (7x10^1) + (5x10^0)
any # to the zero power is one
another example of expanded notation:
492= 400+ 90+ 2
= (4x100) + (9x10) +(2x1)
= (4x10^2) +(9x10^1)+ (2x10^0)
