によって Mercedes delepiani 2年前.
167
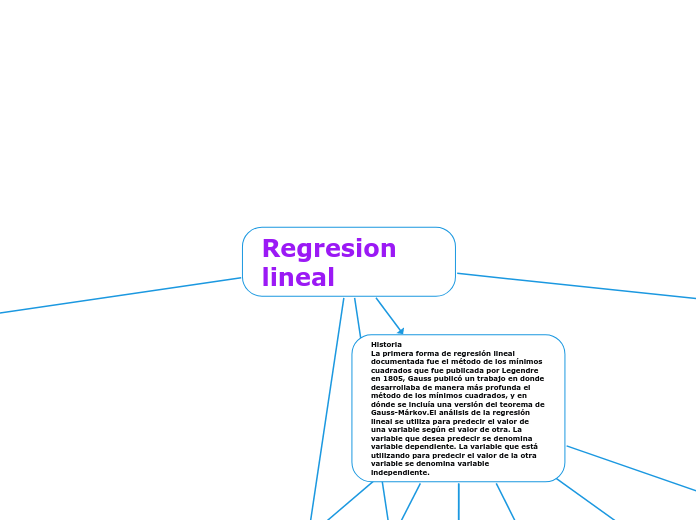
Regresion lineal
La regresión lineal es una técnica estadística utilizada para modelar la relación entre una variable dependiente y una o más variables independientes. Esta relación se representa mediante una ecuación lineal que se ajusta a los datos observados, permitiendo así predecir el valor de la variable dependiente en función de las independientes.