によって Gabriella Rezende 2年前.
336
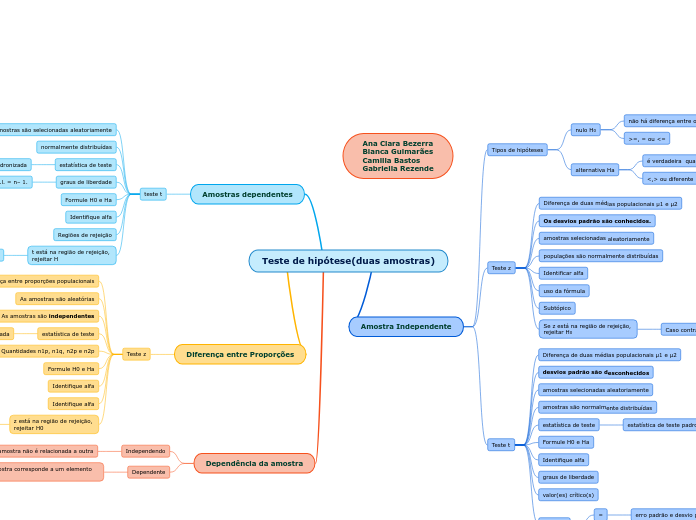
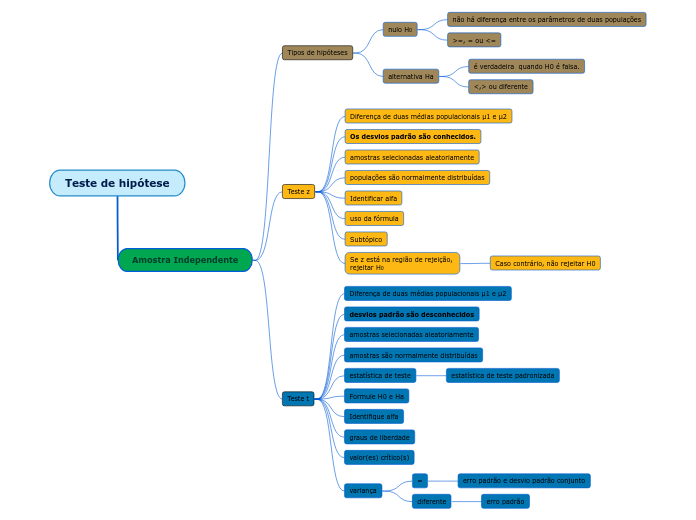
Teste de hipótese(duas amostras)
Em análises estatísticas, o teste de hipótese envolve a avaliação de duas amostras, que podem ser dependentes ou independentes. Para amostras dependentes, utiliza-se o teste t, onde a decisão de rejeitar ou não a hipótese nula H0 depende da região de rejeição.