by Сюникаева Александра 5 years ago
497
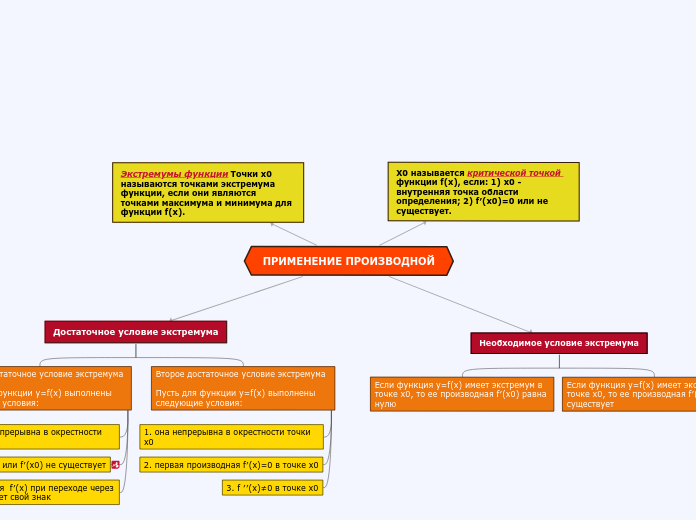
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
The concept of extremum points in a function is crucial in mathematics. These points, known as x0, represent the maximum and minimum values that a function f(x) can attain. For x0 to be considered a critical point, it must either be an internal point within the function'