Отображение - это соответствие между элементами множеств х и у.
Множество всех элементов у∈В, соответствующих элементу х∈А называется образом элемента х.
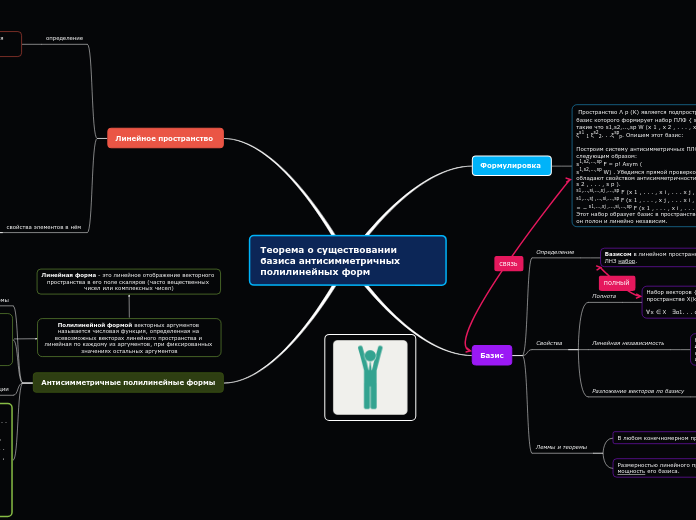
Теорема о существовании базиса антисимметричных полилинейных форм
Антисимметричные полилинейные формы
Пусть W ∈ Ωp0 , тогда
V (x 1 , x 2 , . . . , x p ) =1/p!· Σσ(−1)[σ] W (x σ(1) , x σ(2) , . . . , xσ(p) )-антисимметричная ПЛФ из Λ p(K). Пусть χ ∈ S n - произвольная перестановка тогда V(x χ(1), x χ(2) , . . . , x χ(p) ) =1/p!·∑σ(−1)[σ] · W(x σ◦χ(1) , x σ◦χ(2) , . . . , x σ◦χ(p) ) =1/p!·∑φ◦χ−1(−1)[φ◦χ−1] · W(x φ(1) , xφ(2) , . . . , x φ(p) ) = (−1)[χ−1] ·1/p!·∑φ(−1)[φ] W(x φ(1) , x φ(2) , . . . , x φ(p) ) = (−1) [χ] · V (x 1 , x 2 , . . . , x p ) Операция изготовления антисимметричной ПЛФ V из произвольной ПЛФ W называется операцией антисимметризации формы W. Для нее пишут
V = Asym W
процесс антисимметризации
Полилинейная форма V ∈ Ωp0 (K) называется антисимметричной, если она меняет знак при транспозиции любых двух ее аргументов или V (x 1 , x 2 , . . . , x p ) = (−1)[σ]
V (x σ(1) , x σ(2) , . . . , x σ(p) ), σ ∈ S n .
Транспозиция - это перестановка, при которой переставляются местами только два элемента множества.
Перестановкой на множестве элементов называется биекция множества {1,2,3,4...n} на себя.
Биекция - это отображение, которое является одновременно и сюръективным , и инъективным
Сюръекция - это отображение множества х на множество у, при котором каждый элемент множества у является образом хотя бы одного элемента множества х.
Инъекция - это отображение множества х в множество у, при котором разные элементы множества х переводятся в разные элементы множества у.
Полилинейной формой векторных аргументов называется числовая функция, определенная на всевозможных векторах линейного пространства и линейная по каждому из аргументов, при фиксированных значениях остальных аргументов
Линейная форма - это линейное отображение векторного пространства в его поле скаляров (часто вещественных чисел или комплексных чисел)
Для того, чтобы ПЛФ была антисимметричной необходимо и достаточно, чтобы она обращалась в ноль при совпадении любых двух ее аргументов:
V ∈ Λp(K) ⇔ V (x 1 , . . . , x i , . . . , x i , . . . , x p ) = 0.
полилинейные формы
Линейное пространство
свойства элементов в нём
Ассоциативность
α(βx) = (αβ)x = β(αx)
Существование единицы по умножению
∃1 ∈ K :
1 · x = x
∀x, y, z ∈ R:
x · (y + z) = xy + xz
определение
Линейным пространством X над полем K называется модуль над кольцом, имеющим также алгебраическую структуру поля
Полем называется ненулевое кольцо, в котором каждый ненулевой элемент обратим
Модулем над кольцом R называется абелева группа (G, +) с заданной бинарной операцией R × G → G, записываемой как (α, x) → αx и согласованной действующей на групповой структуре на G
Абелева группа - группа, в которой операция является коммутативной a*b=b*a
Группа - это множество если закон композиции, заданный на множестве удовлетворяет следующим аксиомам:
существование нейтрального элемента
e ◦ x = x
для каждого элемента существует обратный
z ◦ x = e,
где z - это обратный, а e - нейтральный
ассоциативность закона
Кольцом R называется множество замкнутое относительно двух согласованно заданных на нем бинарных операций, удовлетворяющих следующим аксиомам
аксиомы:
Существование единицы
∃ 1 ∈ R :
1 · x = x = x · 1
Коммутативность
∀x, y ∈ R
x · y = y · x
Дистрибутивность
∀x, y, z ∈ R:
x · (y + z) = xy + xz
Существование нуля
∀x ∈ R ∃ 0 ∈ R :
x + 0 = x = 0 + x
Асоциативность умножения
∀x, y, z ∈ R
(xy)z = x(yz)
Существование противоположного
∀x ∈ R ∃ (−x) :
x + (−1) = 0 = (−x) + x
Ассоциативность сложения
∀x, y, z ∈ R
(x + y) + z = x + (y + z)
Согласованное действие:
∀α ∈ R, ∀x1, x2 ∈ G
α(x1 + x2) = αx1 + αx2
Действие кольца в группе
∀α, β ∈ R, ∀x ∈ G
(α + β)x = αx + βx, (αβ)x = α(βx)
Базис
Леммы и теоремы
Размерностью линейного пространства X(k) называется мощность его базиса.
Мощность - характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества
В любом конечномерном пространстве существует базис.
Свойства
Разложение векторов по базису
Пусть {ei}n i=1 - базис линейного пространства X. Тогда
∃ {ξi ∈ K}ni=1 : x = Σni=1 ξiei ∀x ∈ X.
Набор чисел {ξi}ni=1 называется координатами вектора x в базисе {ei}ni=1.
Линейная независимость
Набор векторов {xi}ni=1 называется линейнонезависимым (ЛНЗ), если:
α1x1 + α2x2 + . . . + αnxn = 0.
имеет место только тогда, когда α1 = α2 = . . . = αn = 0.
Полнота
Набор векторов {xi}mi=1 называется полным в линейном пространстве X(k), если выполняется следующее условие:
∀x ∈ X ∃α1. . . αn: x = Σni=1 αixi
Определение
Базисом в линейном пространстве X(k) называется полный ЛНЗ набор.
Формулировка
Пространство Λ p (K) является подпространством Ωp0(K), базис которого формирует набор ПЛФ { s1,s2,...,sp W} такие что s1,s2,...,sp W (x 1 , x 2 , . . . , x p ) = ξs1 1 ξs22. . .ξspp. Опишем этот базис:
Построим систему антисимметричных ПЛФ { s1,s2,...,sp F}, следующим образом:
s1,s2,...,sp F = p! Asym (
s1,s2,...,sp W) . Убедимся прямой проверкой, что эти ПЛФ обладают свойством антисимметричности по индексам (s 1 , s 2 , . . . , s p ). s1,...,si,...,sj ,...,sp F (x 1 , . . . , x i , . . . x j , . . . , x p ) =
s1,...,sj ,...,si,...,sp F (x 1 , . . . , x j , . . . x i , . . . , x p ) =
= − s1,...,sj ,...,si,...,sp F (x 1 , . . . , x i , . . . x j , . . . , x p ) . Этот набор образует базис в пространстве Λ p (K), так как он полон и линейно независим.
Набор - конечная и
упорядоченная совокупность его элементов