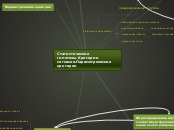
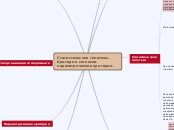
Статистические гипотезы.Критерии согласия.Параметрические критерии
Критерии согласия
Критерий Шапиро-Уилка
объем выборки не более 50
лучший критерий нормальности
Критерий Колмогорова-Смирнова
выборка принадлежит ген.совокупности с норм. распределением
степень согласия стат. распределения с гипотет. распределением
Параметрические критерии
применение возможно если
генеральные дисперсии равны
выборки извлечены из нормально распределенных генеральных совокупностей
Критерий Стьюдента
две зависимые выборки
две независимые выборки
Н0 не отвергается
фактор не влияет на исследуемую величину
выборочные средние различаются не значительно
генеральные средние равны
Н0 отвергается
фактор влияет на исследуемую еличину
выборочные средние различаются значимо
ген. средние не равны
Критерий Фишера-Снедекора
Н1 генеральные дисперсии не равны
нулевую гипотезу отвергаем
дисперсии различаются значимо
Н0 генеральные дисперсии равны
нулевую гипотезу не отвергаем
дисперсии различаются не значимо
сравнить точность двух приборов
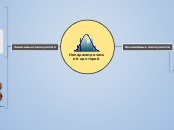
нормальный закон распределения
больше отклонение от среднего значения, меньше частота встречаемости
совпадение
медиана
мода
средняя арифметическая
правило 3х сигм
нормальное распределение не далее чем на 3 сигмы(99,7%)
тип организации эксперимента
зависимые выборки
оказывает влияние
независимые выборки
не оказывает влияния
Виды критериев
непараметрические
используются выборочные данные
параметрические
параметры выборки
Н1 не соответствует функции нормального распределения
Н0 распределение изуч. величины соответствует функции нормального распределения
это предположение о виде неизвестного распределения
альтернативная H1
проверка статистических гипотез
р больше 0,05 Н0 не отвергаем
р меньше 0,05 Н0 отвергаем
Н0 не верна, но не отвергается
статистическая ошибка 2 рода
Н0 не верна и отвергается
Н0 верна , но отвергается
статистическая ошибка 1 рода
Н0 верна и не отвергается
нулевая H0
проверка основной гипотезы
статистический критерий
критические точки
критическая область
отвергается нулевая гипотеза
допустимая область
не противоречит нулевой гипотезе
наблюдаемое значение критерия
статистическая гипотеза
объем выборки
репрезентативная
выборочная совокупность
множество объектов из
объем генеральной совокупности
число объектов
гениральная совокупность
объекты с изучаемым признаком