by Francisco Santana 11 years ago
195
More like this
y=yoe^ct^
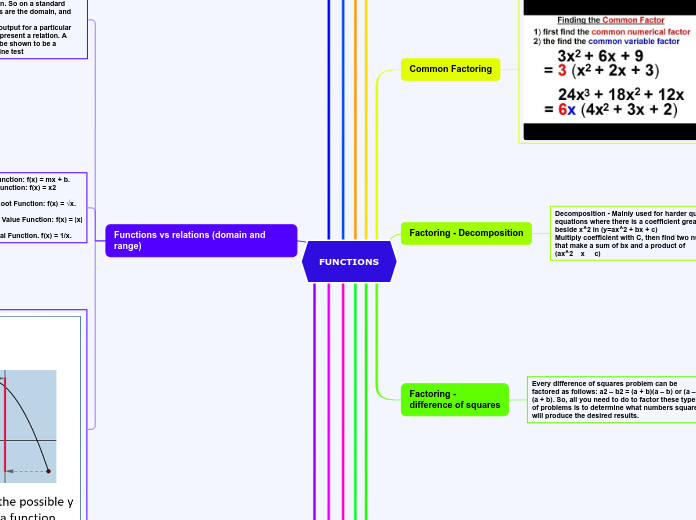
Theorem 7.28 Dx a^x^= a^x^=lna
Theorem 7.29 ∫a^x^ dx=(1/lna)a^x^ +C
Theorem 7.31 Dx log_a_x= Dx (lnx/lna)=i/xlna
∫1/u du=ln
∫e^x^ dx=e^x^
trig integrals
(i)∫tanu du= -ln {cosu} +C
(ii)∫cotu du=ln {sinu} +C
(iii)∫secu du= ln {secu+tanu} +C
(iv)∫cscu du=ln {cscu-cotu} +C
If x is any real #, then e^x^=y iff lny=x
If p and q are real #s and r is a rational #, then:
(i)e^p^e^q^= e^p+q^
(ii)e^p^/e^q^=e^p-^
(iii)(e^p^)^r^=e^pr^
Dx e^x^=e^x^
y=f(x)
lny=lnf(x)
Dx[lny]=Dx[f(x)]
1/yDxy=Dx[lnf(x)]
Dxy=f(x)Dx[lnf(x)]
If p>0 and q>0, then:
(i) lnpq=lnp+lnq
(ii) lnp/q=lnp-lnq
(iii) lnp^r6=rlnp for every rational # r
Definition 7.9: natural log, ln, is defined by lnx= integeral from 1 to x of 1/t dt for every x>0
Theorem 7.10: Dx lnx=1/x
If a differntiable function f has an inverse function g=f^-1^ and if f'(g(c))=/=0, then g is differentiable at c and g'(c)=[1/f'(g(c))]
Definition 7.1: A Function f with domain D & range R is a one-to-one fucntion whenever a=/=b in D, then f(a)=/=f(b) in R
Definition 7.2: Let f be a one-to-one function with domain D and range R. a fucntion g with domiain R and range D it the inverse function of f, provided the folloing contition is true for every x in D and every y in R; y=f(x) iff x=g(y)
(i) sin(arcsinx)=x if -1≤x≤1
(ii) arcsin(sinx)=x if -
