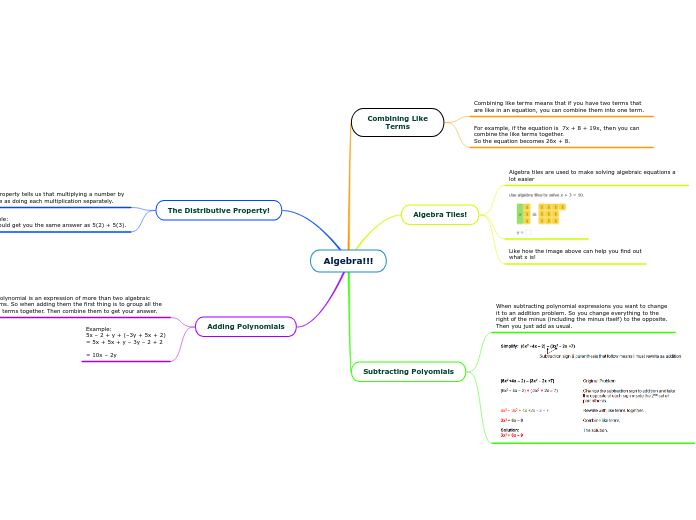
Graphing
Does the equation have an exponent?
No.
Than it is a linear equation.
Use Algebra to put it in slope-intercept form.
If you can't put it in slope-intercept form
than perhaps it can be put in this form
y=|x|+D, in which case it is an absolute value
Yes.
Use algebra to put it in the form of
Ax^2+Bx+C=y
If quadratic, can it be factored easily?
If not, use the quadratic equation
to find the zeros
x equals negative B plus or minus
square root B squared minus four A*C
all over two A. Where A,B and C are
defined by the standard form of a
quadratic equation as written above.
Be careful not to drop negative signs
Remember that you cannot take
the square root of a negative number
If everything under the
radical is negative, the
graph does not intersect
the x-axis. (everything
under the radical is called
the descriminant because
it descriminates between
3 forms of quadratics.
Those with two zeros and
a positive determinant,
those with one zero and
a determinant of zero,
and those with no zeros
and a negative determinant)
When you have finished solving the
quadratic formula, x will equal the
zeros of the function. In other words,
you have now located where the
graph of the equation intersects the x-axis.
If there are no zeros
(negative descriminant)
than skip this step for
now and move on to
the next step.
Plot the Zeros on the coordinate
plane. (aka. graph the points
of the x-intercepts)
Find the axis of symmetry by
using the equation x=-b/2a
and the definition of A, B and
C as defined in the beginning.
Use this new x-value to find its
cooresponding y-value by
plugging the x-value into the
original equation and solving for y.
These x and y values are the
coordinants of the vertex of
the quadratic equation.
You can now plot this point
on your graph.
You now must use your
knowledge of what the
parent function of quadratic
equations looks like to finish
drawing your graph.
If yes, than factor it.
Once it has been factored,
set the equation equal to zero
by replacing "y" with zero.
Find the "zeros" of the function
by splitting it into two equations
that are both equal to zero and
solving them.
x will now equal the zeros
of the function. In other words,
you have now located where
the graph of the equation
intersects the x-axis.
If it cannot be put in this form,
than it is not linear or quadratic