Kristin Johnson

More like this

MAT.126 1.4-1.5

by David Kedrowski

Trigonometric Functions and their Identities

by Jessica Gvc

exponential and logarithmic functions

by Maryam Alameri

Math 252

by Javone McClelland

Key ideas:

Why is it important to teach students algebraic reasoning, and graphing? Why do student's need to make connections with geometry?  Forty years from now, four plus four will still equal eight.  Students need critical thinking skills so they can think through an issue, and reason logically to solve problems in the real world.

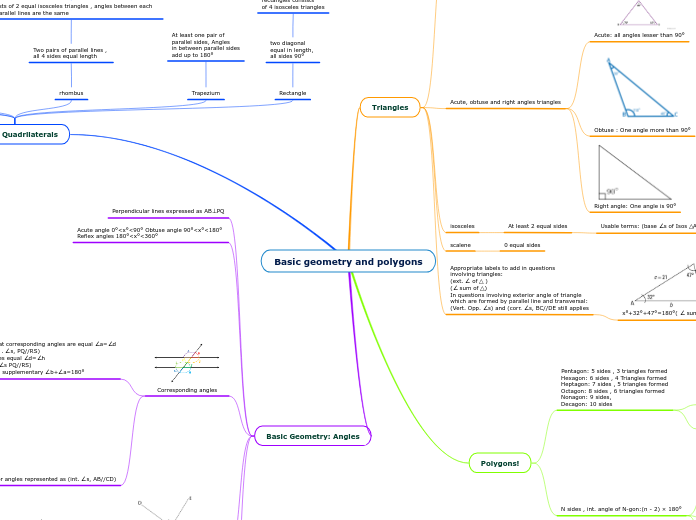
Teaching Algebraic Reasoning, Graphing, and Connections with Geometry

Teaching algebraic reasoning, graphing, and making connections with geometry can be confusing.  The map is packed with tools to help a teacher.  It includes games, videos, lesson plans, and tools to help your students succeed. 

The map can also refresh those skills that may have been forgotten.  The mind map will keep you organized and shows you how key concepts can be chunked together.  

Additional References

References:

Alex Lesson Plans. Alabama Learning Exchange. Retrieved from

http://alex.state.al.us/lesson_view.php?id=26338

https://www.youtube.com/watch?v=k4KdGiJPbN8

Basics About a Circle.

http://www.areacircle.com/basics-about-area-of-a-circle.html

Basic Algebra. Basic Mathematics. Retrieved from

Lesson Plans and Additional Resources

Modeling with Mathematics

Graphing Two Variables to Express Algebraic Relationship

Algebra, geometry are not tow separate areas.  Many of the same applications apply to both. 

Graphing Linear Functions Worksheet

Teacher Channel Video

Function Tables

Function tables are lists of possible values of a variable and the function's result.

Alex Learning Lessons

Graphing Points, Lines, and Elementary Functions

Nonlinear Funtions

- A non-linear function is a not a linear function.

- A quadratic function is


f (x) = ax 2 + bx + c , where a, b, c if

a≠ 0 .


-Exponential function (see video)

Equations of Lines

First before beginning any computation it is important to

1. Make sure you understand the problem.

2. Devise a plan t help with the problem.

3. Carry out the plan or compute the problem.

4. Look back at how we solved the problem. 

We need to study the problem to have a better understanding of what we are being asked.  We need to decide how to solve it.  Then it is important to being to solve it.  Then reflect and look back at the solution.

What Theorem needs to be used.

1. The point-slope form is will be used when we are given a point (x1, y1) and a slope m.  Then the numbers are plugged into the formula:

y – y1 = m(x – x1)

2. The slope-intercept form is used where m is the slope and b is the y-intercept.

y=mx+b

3 For the two-point form of the equation of a line we would use the formula

y – y1 = m(x – x1)

The slope and (x1, y1) is a point on the line. Point-slope is the form used most often when finding the equation of a line.

Functions:

-A linear function is a straight-line graph.

Slope

What is the slope? A real world example is walking up or down a flight of stairs.

The slope of a line defines the steepness of the line.  It allows us to know if the line is rising or falling.

Slope =  Rise
             Run

 

The Distance Formula

We can use this formula to determine the distance between the two points (5,5) and (1,2) by using the formula.

The Cartesian Coordinate Plane

Quadrant I both coordinates are positive.

Quadrant II first coordinate is negative and second coordinate is positive.

Quadrant III both coordinates are negative.

Quadrant IV first coordinate is positive and second coordinate is negative.

Plotting points

Example of Graph Quadrants

References

References:

Ehow. How to Use Functions to Teach Algebra. Retrieved from http://www.bing.com/videos/search?q=how+to+use+functions+tables+youtube&FORM=VIRE7#view=detail&mid=D23955324C10AFD5B81ED23955324C10AFD5B81E

Graph Game. Retrieved fromﾠ

http://www.mathxl.com/Student/MediaPopup.aspx?type=assignedmedia&assignmentId=283516755&loc=3&flush=yes&record=1&OnOpenerViewed=doMedia_onViewed

Graphic. Retrieved from http://www.jackanderica.com/math/images/plot007.jpg

IXL.

http://www.ixl.com/math/grade-3/solve-for-the-variable-addition-and-subtraction-only

ﾠ

Long, C. et al. (2015). Mathematics Reasoning for Elementary Teachers. Boston, MA. Pearson

Math Help. Mapping Diagrams. Retrieved from http://www.bing.com/videos/search?q=functions+as+arrow+diagrams+video+algebra&FORM=VIRE5#view=detail&mid=49B4EB35DDBD9F4C138949B4EB35DDBD9F4C1389

Math Plant. Retrieved from

http://www.mathplanet.com/education/algebra-1/discovering-expressions,-equations-and-functions/expressions-and-variables

Math XL. Retrieved from http://www.mathxl.com/Student/MediaPopup.aspx?type=assignedmedia&assignmentId=283516755&loc=4&flush=yes&record=1&OnOpenerViewed=doMedia_onViewed

Solving Equations. Retrieved from http://www.sosmath.com/algebra/solve/solve0/solve0.html

Think Math. Retrieved from

http://thinkmath.edc.org/resource/guess-my-rule

References:

Ehow. How to Use Functions to Teach Algebra. Retrieved from http://www.bing.com/videos/search?q=how+to+use+functions+tables+youtube&FORM=VIRE7#view=detail&mid=D23955324C10AFD5B81ED23955324C10AFD5B81E

Graph Game. Retrieved from

http://www.mathxl.com/Student/MediaPopup.aspx?type=assignedmedia&assignmentId=283516755&loc=3&flush=yes&record=1&OnOpenerViewed=doMedia_onViewed

Graphic. Retrieved from http://www.jackanderica.com/math/images/plot007.jpg

IXL. Retrieved from 

http://www.ixl.com/math/grade-3/solve-for-the-variable-addition-and-subtraction-only

Connection between Algebra and Geometry

Math is integrated into many different areas such as geometry, probability, and algebra.  They will continue to keep building on one another.

Circles

Picture a circle and you are standing in the center of it.  If you were to run from the center to the outside edge in a straight line that distance is the radius.

Using the circle analogy again, if you were to run in a straight line through the center of the circle and end on the other side this would be the diameter.

Using a circle and running around edge of the circle is called the circumference.

Parallel and Perpendicular Lines

Parallel lines are parallel if they are always the same distance apart and will never meet. Therefore, their slopes are always the same.

Perpendicular lines are if they meet at a right angle (90°). 

Variables, Algebraic Expressions, and Connections with Geometry

Describing and Visualizing Functions

We can solve equations by using visual functions such as "What's my rule, function tables, arrow diagrams, machines, and graphs."

Example as graphs

A graph allows you to visualize data sets. 

Example of the Fibonacci sequence and the doubling function

Example Functions as arrow diagrams

Example for Function as tables

A math function table is a table used to plot possible outcomes.

Example Functions as formulas

Defining and Visualizing Functions

The definition of function requires that a single value y be assigned to each x-value in the domain.

Example,

We are at the gas station, filling the vehicle with gas which is priced at $3.95 per gallon.  As we know from filling our gas tank that day the amount is a function of the amount of gas purchased.  Letting the variable (output) represent the final bill in dollars and cents, then y is defined by the rule y=3.95s.  Machines help us compute this formula into a dollar amount

"How much does 15 gallons cost?" The answer is $59.25.  This is the only cost of the gas because there is only one value for y for each x. 

Solving Equations

An equation is a mathematical expression starting that two algebraic expressions have the same value.

Algebraic Expressions

Algebraic expression is a representation that involves variables, numbers, and operations symbols.

The cost of a gallon of milk in the store is increased by 20 cents.  What is the cost of a gallon of milk that used to cost c dollars? What is the old cost of the old gallon of milk that now costs d dollars?

Answer:

c+0.20

d-.20 (in dollars)

Variables

Lets start with algebraic reasoning.  Here are some topics we will cover.

• What are variables?

• How to form algebraic expressions involving variables, numbers, and operation symbols?

• What is the definition and visualization of functions

Variables used in algebra are letters such as x, y, f, or any letter to represent unknown numbers.

Variables express formulas

COMMONLY USED FORMULAS

1,  Distance


Variables:

d= distance traveled
r= rate of travel (speed)
t= time of travel


Formula: d = rt

2.  Perimeter of a rectangle


Variables:

p = perimeter
l= length
w= width


Formula: P = 2L + 2W


3.  Area of a rectangle


Variables:

A= area


Formula: A= LW

Variables serve as unknowns in equations

Find a number to place in the blank that makes the sentence true.

__ + 7 = 9

or

(3x-6)(x-2)=0
 

Variables express relationships

Variables express relationships here are some examples.

 J=K-6 ("Addy is six years younger than Kendra")


K=J+6 ("Sara is six years older than Addy.")


K-J=6 ("The difference in age between Sara and her younger sister Addy is six years.")

Variables describe generalized properties

Example

Example:


a(b+C) = ab+ac

Constants

A constant is a non-changing value that represents a fixed number. 

Here are several examples of a constant

3, 10, π, 1/2.

Examples

There are 12 in a dozen of eggs

There are four sides of a rectangle

and

2 + 5 = 7