Math - Chapter 5

More like this

Elementary Mathematics

by Jacklyn Martinez

MTE 280 Investigating

by Epimenio Negrete Jr

Factoring

by Kelsey Hinkel

Quadratic Equations By. Eshal Khaliq

by Khaliq Eshal

Perfect square trinomials

Square root of a and the square root of c all multiplied by 2 is equal to b

4x² + 12x + 9

Square root of 4 -> 2 square root of 9 is -> 3

2(2)(3)

= 12 = b

∴ This is a perfect square trinomial

(2x+3)²

(3x+4)(8x+5)

24x² + 15x + 32x + 20

24x² + 47x + 20

Floating topic

used to simplify equations/expressions

done so by finding the greatest common factor in an expression/equation

Math - Chapter 5

Expanding

squaring binomials

(a+b)²

can be solved in 2 ways

(a+b)(a+b)

Subtopic

FOIL it

a²+ab+ab+b²

using Formula

a² - 2ab+b²

(a-b)²

a²+2ab+b²

Short form

distributive property

multiply a single term by 2 or more terms

used to expand equations/expressions

Multiply binomials

methods to do this

FOIL

F - First O - Outer I - Inner L - Last

its like applying the distributive property twice

multiply each term in the first factor by each in the second

2 factors of 2 terms being multiplied to each other

(x-4)(x-5)

difference of squares

part of factoring as well

(4x+5y)(4x-5y)

simplifies to

(4x)² - (5y)²

16x² - 25y²

(a+b)(a-b)

all term a = to the same thing all term b = to the same thing

a² - b²

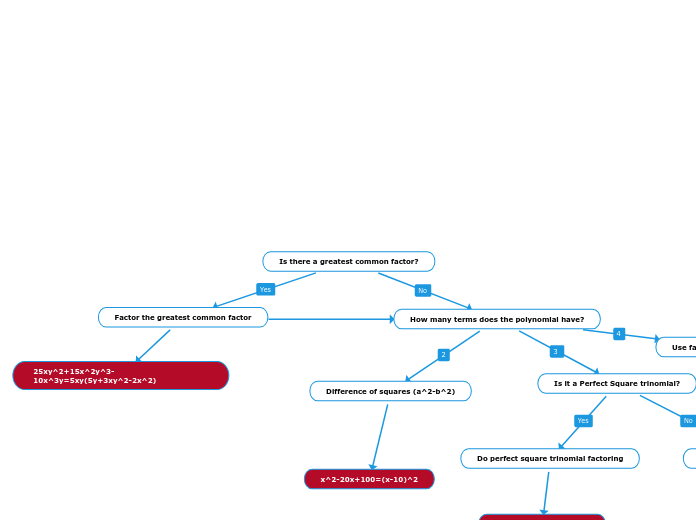
Factoring

Factoring Quadratic expressions (a=1)

find 2 integers that when multiplied is equal to c

those 2 integers have to also equal to b when added together

ax² + 5x +6

__ x __ = 6 (c) __ + __ = 5 (b)

Those two integers are 2 and 3

2 x 3 = 6 (c) 2 + 3 = 5 (b)

r = 2 s = 3

(x+2)(x+3)

can be switched around

r ans s can equal to which ever integer

always see if you can common factor something out first

in this case no

where a, b, and c are integers

in this case a is equal to one

Factoring Quadratic expressions (a≠1)

ax² + bx + c

Where a, b, c are integers

Find 2 integers that when multiplied together is equal to a X c

Those same two integers have to add up to b

a(x+r)(x+s)

3x² + 8x +4

__ x __ = 12 ( a X c) __ + __ = 8 (b)

Those two integers are 2 and 6

2 x 6 = 12 (a X c) 2 + 6 = 8 (b)

Break down b into 2x and 6x and add that to the equation

3x² + 2x + 6x +4

Group factor

x(3x+2) + 2(3x+2)

(3x+2)(x+2)

refer to group factoring

Group common factors

4 terms separated into 2 groups

find common factor for both groups

produces a binomial common factor

2wx + 10w +7x + 35 l_________l l______l group one Group two

Group 2 -> 7 is the greatest common factor

7(x+5)

Group one -> 2 and w = greatest common factor

2w(x+5)

2w(x+5) + 7(x+5)

binomial common factor

refer to binomial common factor

(x+5)(2w+7)

Binomial common factors

A binomial factor that is shared by all the terms of a polynomial

common binomial among a polynomial

7(x-3) - 2x (x-3)

(x-3) is the greatest common factor

(x-3) [ 7(x-3) 2x (x-3)] ______ - ______ (x-3) (x-3)

(x-3)(7 - 2x)

When (x-3) is removed from the terms

(7-2x)

divide everything by (x-3)

put it outside the bracket

∴ equation not changed

Binomial = 2 terms

Monomial common factors

factor out a monomial out of a set of terms

6x² - 14x + 8

the biggest number that can divide all of these terms is 2

no biggest common variable

2 is the only thing common among all 3 terms

divide everything by 2

6x² - 14x + 8 ___________ 2

2(3x² - 7x + 4)

you cannot change the equation

that's why the 2 is put in the front of the brackets

if you ere to expand it you would end up with the same equation as before

nothing was changed

only simplified

Monomial = 1 term