by Emma Delong 3 years ago
194
More like this
Scientific Notation:
Used for very large or very small numbers - a way to write numbers so that it is easier to manipulate.
Scientific Notation always has:
Positive exponents equal a large number (greater than 1).
Negative exponents equal a small number (between 0 and 1).
Example:
125,000,000
since this is a large number the exponent will be positive. Move the decimal place between the first 2 non-zero digits. Count the places that the decimals have moved to find the exponent.
125000000 is equal to 1.25 x 10^8
Order of Operations:
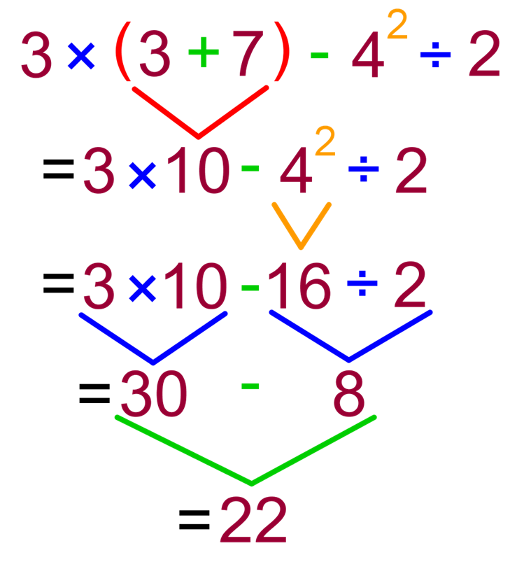
Instead of PEMDAS, use Groupings, exponents, Division/multiplication (left to right), Subtraction/ Addition (left to right). This method helps students understand that the order of multiplication/division does not matter and the order of subtraction/addition does not matter.
First, identify all groupings and mark them on the problem. Next, follow the steps listed above, completing the groupings first, then exponents, Division/multiplication (left to right), and Subtraction/ Addition (left to right).
Bring down the answers to each step to solve the entire problem.
Example:
Adding Decimals:
**always estimate the answer before solving problem**
First, Line up the whole numbers.
Then, solve to find the final answer.
Finally, check to make sure the answer is close to estimation.
Subtracting Decimals:
**always estimate the answer before solving problem**
First, line up the whole numbers.
Then, solve to find the final answer.
Finally, check to make sure the answer is close to estimation.
Multiplying Decimals:
**always estimate the answer before solving problem**
First, multiply without decimals.
Next, reach the answer without decimals and add the decimal in closest to the estimated answer. (If the estimate was 10 and the answer without decimals is 10938, place the decimal between 0 and 9.)
Finally, check to make sure the answer is close to estimation.
Showing Addition of Decimals:
Use base ten blocks (or draw) to show adding of decimals. Make sure to reiterate that rods are tenths (not ten whole units) and one unit blocks are hundredths.
Showing Subtraction of Decimals:
Use base ten blocks (or draw) to show subtraction of decimals. First, draw the first number, then circle to remove the second number.
Showing Multiplication of Decimals:
Use base ten blocks (or draw) to show multiplying of decimals. Draw out the numbers using verticle lines for one number and horizontal for the second number. The double shaded areas represent the final answer.
Showing Addition:
Draw two similar size boxes and fill out the boxes to represent the fraction.
Next, draw lines in each box to correspond with the piece size of the other fraction.
Finally, draw a third box with lines that match the other two boxes. Fill out the third box with the same number of shaded pieces from the other boxes (combined).
This will give the final answer.
Showing Subtraction:
Draw two similar size boxes and fill out the boxes to represent the fraction.
Next, draw lines in each box to correspond with the piece size of the other fraction.
Next, subtract the shaded in portions of the second box from the first by drawing an X through each piece. The unmarked (no X) pieces represent the final answer.
Showing Multiplication:
Draw one large box and shade in for the first fraction.
On the same box, use a different color (different than the first fraction) to draw the lines for the second fraction and to shade in the fraction.
The double shaded areas that are created represent the final answer.
Multiply Fraction Algorithms:
First, break the denominators and numerators down into their factors.
Next, Identify funky ones (any numerator that is the same as a denominator becomes a funky one).
Next circle all numbers that have not become funky ones
Finally, multiply all numbers circled numbers in the equation.
*For problems that have whole numbers use the "backward C" (start at the denominator and multiply the denominator by the whole number then add the numerator). *
**Attached video shows algorithm and visual representation of multiplying fractions**
Dividing Fractions Algorithms:
First, keep the first fraction the same, change the division sign to multiplication, and flip the second fraction. (keep, change, flip)
Next, solve as you would a multiplication problem.
Break the denominators and numerators down into their factors, Identify funky ones, circle all numbers that have not become funky ones, multiply all numbers circled numbers in the equation.
*Always do the "backward C" first. *
Solving Fractions:
Add or subtract the whole numbers first, then handle the fraction.
If the pieces are the same size (the denominator is the same), add or subtract the numerator and keep the denominator the same.
To address subtraction problems where a fraction is being taken away from a whole number, change the whole number into a fraction.
Different denominators:
With different size denominators, first find out what is in each denominator.
From here we multiply each fraction by what the other denominator has that it does not.
Then solve normally.
Understanding Fractions:
Approach teaching fractions with understanding context. For example, 6 cars are bigger than 6 cats.
What does the top number tell us about the fraction? The top number is the number of pieces (things) we have.
What does the bottom number tell us about the fraction? The bottom number is the size of the pieces we have.
The size of the pieces is inversely related to the size of the denominator/ the bigger the denominator the smaller the size of the pieces.
Solving Subtraction:
Subtraction is the same as "adding the opposite"
Keep the first number the same, change the subtraction sign to addition (- to +), change the sign of the second # to the opposite sign.
Example: 36 - (-41)
Keep the 36 the same, change the subtraction sign to addition, and change the -41 to positive 41. Then solve
36+ 41 =77
Solving Multip/Division:
Remember same signs equal a positive, different signs equal a negative, then solve normally.
Example: (-3)(-8)
Since both numbers are negative the answer will be positive. Solve normally, 3 x 8 equals 24.
Show Subtraction:
Use + and - to write out integer problems. Circle to remove what you are taking away. (shown below as a line through the "takeaways" due to formatting)
For example: 5 - 3
+ + + + +
which leaves you with ++ or 2.
Add zero banks when necessary to solve problems.
Show Multiplication:
Draw out the groups of integers using + and -.
For example: 3(-2) is shown below
-- -- --
This is 3 groups of -2, for an answer of -6.
Building Subtraction:
Best ways to say or think about problems:
When building subtraction use zero banks as necessary to answer problems.
For example, in the problem 4-7, we do not have enough positive counters to remove 7. Therefore, add enough zero banks to allow take away of 7 positives.
Building Multiplication
Best ways to say or think about problems:
When building multiplication, use zero banks as necessary to answer problems.
Adding Integers:
Mini Diagram Algorithm:
Use a mini diagram of + and - signs to show whether to add or subtract and if the answer will be positive or negative.
For example, if the problem is 36 + (-12), draw two + over the 36 as 36 is positive and larger than 12. Draw one - over 12. Next, circle the latter two signs. In this case, one + and one - will be circled. Because these signs are different, we will subtract to find the answer.
36
-12
24
Because there was one + left on the mini diagram, we know the answer will be positive.
In the case the signs in the circle are the same, addition will be used.
For example:
-46 + (-26)
two - signs will be drawn over -46 and one over -26. Then the two latter signs will be circled. Since the signs are the same we will add.
46 + 26 = 72
Since there was one - sign leftover in the mini diagram, the answer will be negative.
-72
Introduction to Integers:
The red side of color counters represents negative #'s, other side represents positive #s. Negative #'s should always be on the bottom and positive #s on top.
Zero pair: one negative and one positive color counter in an equation
Divisibility Rules:
2: even #s, end in 0,2,4,6,8
3: if the sum of the digits is divisible by 3, the # is divisible by 3
4: if the last two digits are divisible by 4 then the entire # is divisible by 4
5: if the last digit is a 5 or 0, it is divisible by 5
6: If the # is divisible by both 2 and 3, it is divisible by 6
8: If the last 3 digits are divisible by 8, then the entire # is divisible by 8
9: if the sum of the digits is divisible by 9, the # is divisible by 9
10: If the last digit is 0, it is divisible by 10
Division Alternate Algorithms:
Best ways to discuss division:
15/3 would be said as 15 divided into 3 groups.
Problems with traditional division (long division):
Repeated Subtraction:
Allows students to work with numbers they are comfortable with. Set up is the same as long division except for a line drawn on the right side.
Multiplication Alt Algorithms:
Expanded Form:
First, expand the numbers, then multiply the expanded numbers starting with the largest numbers, add results together to get the final answer.
Example- 38 x 25
30 + 8
X 20+ 5
600+ 160
+ 150 + 40
750 + 200 = 950
Left to Right:
Based on expanded form without the need to write everything out in expanded form. Multiply the numbers from left to right, then add together the results to get the final answer.
Example: 38 x 25
38
X25 First multiply 20 x 30, then 20 x 8, then 5x30, finally 5x 8.
600
160
150
+40 Add everything together to get the final answer
950
Lattice:
Similar to lattice for addition. A box is drawn with 2 lines dividing the box into four sections. One number is written on top and one on the LEFT side. Next, the lattice lines are drawn on the box then the #'s on top of each box are multiplied and the results added together.
Introduction to Multiplication Facts:
Strategies for learning multiplication:
Order to teach multiplication facts:
Alternate Algorithms for Subtraction:
Expanded Form Steps:
Write the equation in expanded form. Example. 325 - 209 is written as 300+20+5
- 200 +0 + 1
Next, subtract going down from left to right (hundreds, tens, ones)
300+20+5
- 200 +0 + 1
100 + 20 + 4
Answer: 124
Equal Addends Steps (Subtractends):
First, rewrite the problem vertically.
173
-107
Next, add (or subtract) the same amount to both numbers to create a friendly number on the bottom.
173+ 3 = 176
-107 +3 = 110
Finally, subtract to find the answer.
176
-110
66
Alternate example:
400 -01 = 399
-319 -01 = 318
399
-318
81
Spiraling content refers to reinforcing and reviewing content throughout a semester. Instead of providing all information about a topic at once, information on topics is given in small units then revisited and built upon later.
