by Marcela Agudelo Acevedo 4 years ago
547
Organigrama
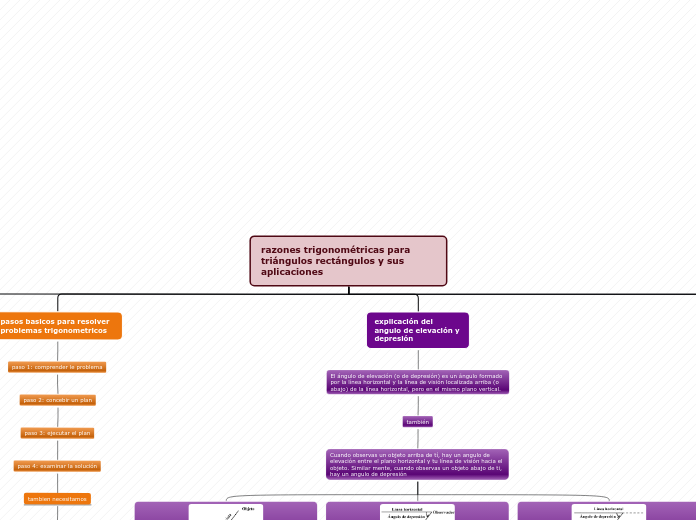
La trigonometría, nacida hace más de 4000 años, ha sido una herramienta esencial para resolver problemas en la vida cotidiana de las civilizaciones antiguas. Sus aplicaciones se extienden a diversos campos de la ciencia y la vida diaria, incluyendo la navegación, la geografía, la astronomía, la arquitectura y todas las ramas de la ingeniería.