by Ronny Romero 1 year ago
103
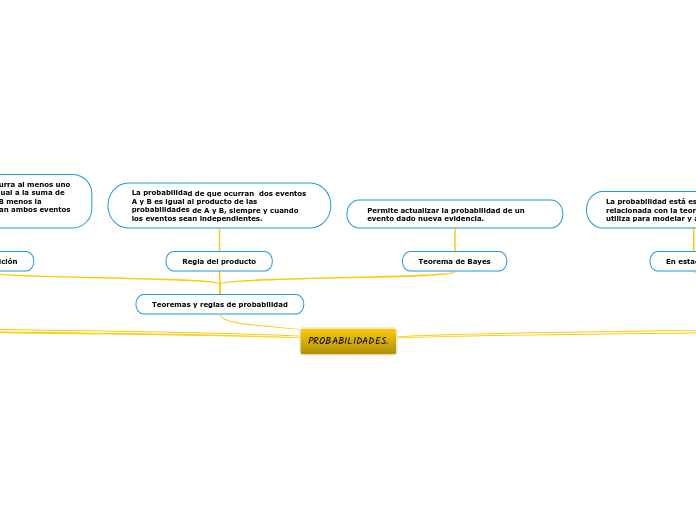
PROBABILIDADES.
La probabilidad es una medida numérica utilizada para cuantificar la posibilidad de que ocurra un evento. Existen varios tipos de probabilidad: la frecuencial se basa en la frecuencia relativa de un evento en un experimento repetido numerosas veces; la clásica se fundamenta en contar los casos favorables y posibles en situaciones de igual probabilidad; la subjetiva depende del juicio personal de un individuo, y la condicional se refiere a la probabilidad de que ocurra un evento dado que otro ya ha sucedido.