Linear and Non-Linear
independent and dependent varialbes
Non-linear relations
points do no lie along a line (curved)
second differences are equal
Linear relations
a straight line
first differences are equal
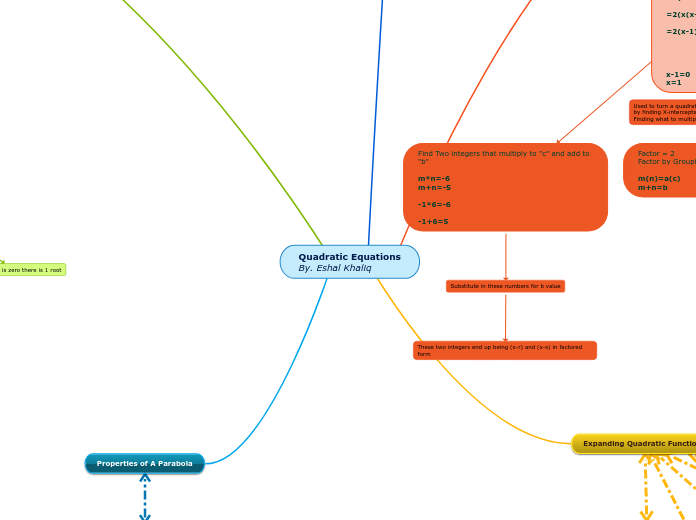
base quadratic
Vertex Form
Quadratic relations
y=ax^2
y=a(x-h)^2 +k
Min/Max Value
if the parabola opens downward it has a max value
if the parabola opens upward it has a min value
y intercept
set x as 0
Zeros
the x intercepts, set y as 0
ex.
The axis of symmetry is the "k" value
Vertical line drawn through the vertex
ex. if the equation was y=-2(x-1)^2 the axis of symmetry would be 1
The vertex of a parabola are the "h" and
"k" values
the point (x,y) where the parabola changes direction
(h,k)
K
H
A
if the value of "a" is negative the parabola opens downward
a=-1
if the value of "a" is positive the parabola opens upward
a=1
Tpes Of Transformations
reflection
A parabola is reflected when the value of "a" is less than 0
a<0
vertical stretch
A parabola is vertically stretched when the value of "a" is more than 1 but less than -1
1
vertical compression
A parabola is vertically compressed when the "a" value is more than -1 but less than 1
-1
vertical translation
Determined by the "k" value in the y=a(x-5)^2+k formula
The value of "k" can shift the parabola vertically up or down
if k<0 then it is translated down
if k>0 then it is translated up
horizontal translation
Determined by the "h" value in the y=a(x-5)^2 +k formula
The value of "h" can shift the parabola horizontally right or left
if h<0 then it is translated the the left
if h>0 then it is translated to the right