by Maxwell He 3 years ago
384
Unit 8: Application of Vectors
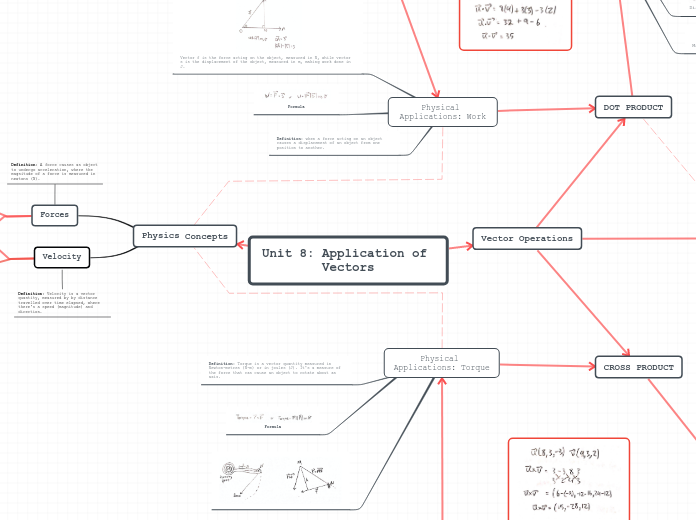
The topic focuses on the application of vectors, covering various fundamental concepts and operations involving vectors in a three-dimensional plane. Direction cosines are introduced, which define the angles a vector makes with the x, y, and z axes.