door ariadna contreras 4 jaren geleden
1311
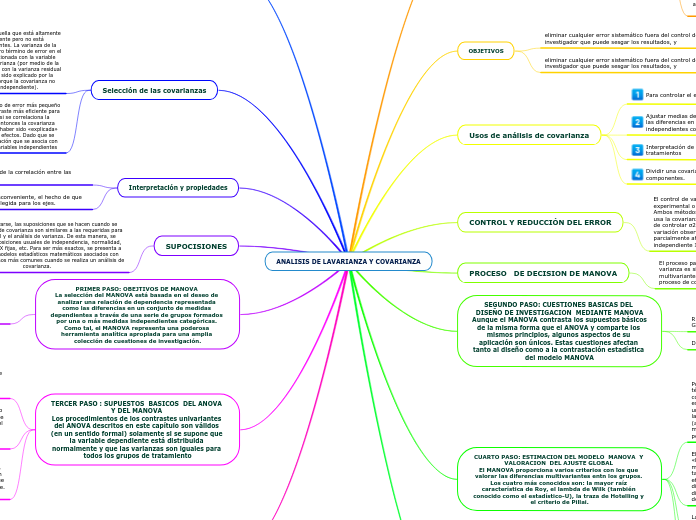
ANALISIS DE LAVARIANZA Y COVARIANZA
El análisis de covarianza y de varianza comparten varias suposiciones, similares a las necesarias para la regresión lineal. Estas incluyen la independencia, la normalidad y la homocedasticidad, entre otras.