door Eunice López 3 jaren geleden
329
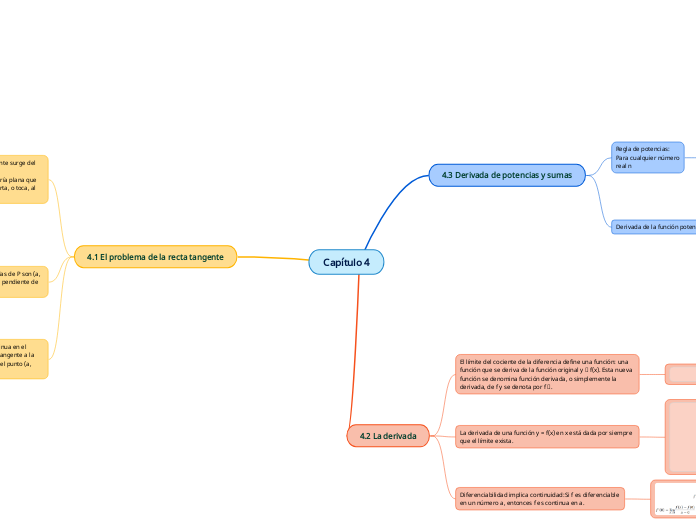
Capítulo 4
El capítulo aborda la derivada de funciones potencias y las reglas asociadas a funciones constantes y la multiplicación por constantes. Explica que la derivada de una función potencia se obtiene multiplicando por el exponente y reduciendo éste en uno.