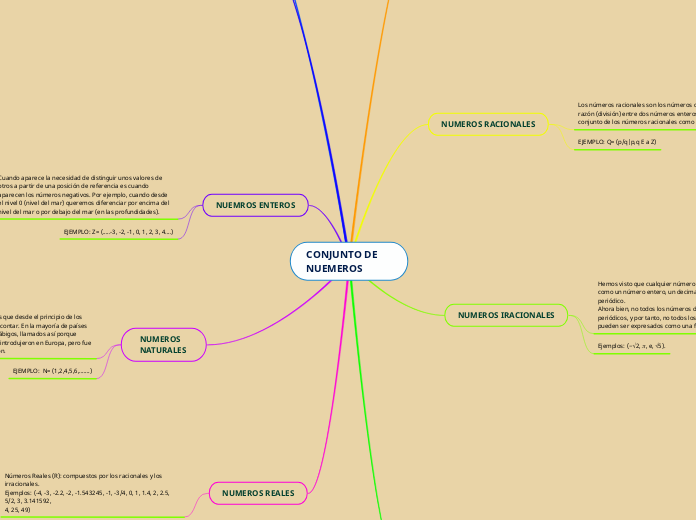
CONJUNTO DE NUEMEROS
NUMEROS REALES
Números Reales (R): compuestos por los racionales y los irracionales.
Ejemplos: (-4, -3, -2.2, -2, -1.543245, -1, -3/4, 0, 1, 1.4, 2, 2.5, 5/2, 3, 3.141592,
4, 25, 49)
NUMEROS NATURALES
EJEMPLO: N= (1,2,4,5,6,.......)
Los números naturales son los que desde el principio de los tiempos se han utilizado para contar. En la mayoría de países han adoptado los números arábigos, llamados así porque fueron los árabes quienes los introdujeron en Europa, pero fue en la India donde se inventaron.
NUEMROS ENTEROS
EJEMPLO: Z= (.....-3, -2, -1, 0, 1, 2, 3, 4....)
Cuando aparece la necesidad de distinguir unos valores de otros a partir de una posición de referencia es cuando aparecen los números negativos. Por ejemplo, cuando desde el nivel 0 (nivel del mar) queremos diferenciar por encima del nivel del mar o por debajo del mar (en las profundidades).
M.C.D
El máximo común divisor es el mayor de los divisores comunes de dos o más números. Para calcularlo se factoriza y se multiplican los factores comunes al menor exponente. Si no los hay el MCD es 1 y se dice que son primos entre sí.
M.C.M
El mínimo común múltiplo (mcm) es la cifra más pequeña que satisface la condición de ser múltiplo de todos los elementos de un conjunto de números.
CONJUNTO NUMERICO
Un conjunto numérico es una parte de un sistema numérico que obedece
también a determinadas reglas y dentro del cual se pueden desarrollar ciertas
operaciones que conducen a otros elementos del sistema o de otros sistemas.
Sobre el conjunto R se definen dos operaciones elementales: la suma (+) y la
multiplicación o producto (·). La suma y el producto de dos números reales es un número
real. Además, se verifican las siguientes propiedades:
- propiedad conmutativa
- propiedad asociativa
- propiedad distributiva
CONMUTATIVA : 𝑎 + 𝑏 = 𝑏 + 𝑎
𝑎 ∙ 𝑏 = 𝑏 ∙ �
56+71=71+56=127
5×6=6×5=30
DISTRIBUTIVA: (𝑎 + 𝑏) ∙ 𝑐 = 𝑎 ∙ 𝑐 + 𝑏 ∙ 𝑐
𝑐 ∙ (𝑎 + 𝑏) = 𝑐 ∙ 𝑎 + 𝑐 ∙ �
2 · (3 + 5) = 2 · 3 + 2 · 5
2 · 8 = 6 + 10
16 = 16
NUMEROS IRACIONALES
Ejemplos: (−√2, 𝜋, e, √5).
Hemos visto que cualquier número racional se puede expresar como un número entero, un decimal exacto o un decimal periódico.
Ahora bien, no todos los números decimales son exactos o periódicos, y por tanto, no todos los números decimales pueden ser expresados como una fracción de dos enteros.
NUMEROS RACIONALES
EJEMPLO: Q= (p/q|p,q E a Z)
Los números racionales son los números que resultan de la razón (división) entre dos números enteros. Se denota el conjunto de los números racionales como
POTENCIACIÓN
Una Potencia es una multiplicación de un número por sí mismo el número de
veces que indica el exponente de la expresión.
PROPIEDADES DE LA POTENCIACION
Multiplicación de potencias con la misma base
Potencias de Potencias
Potencias de Multiplicaciones
Potencia de una Fracción
Subtopic
