door luis yael sanchez 8 jaren geleden
1534
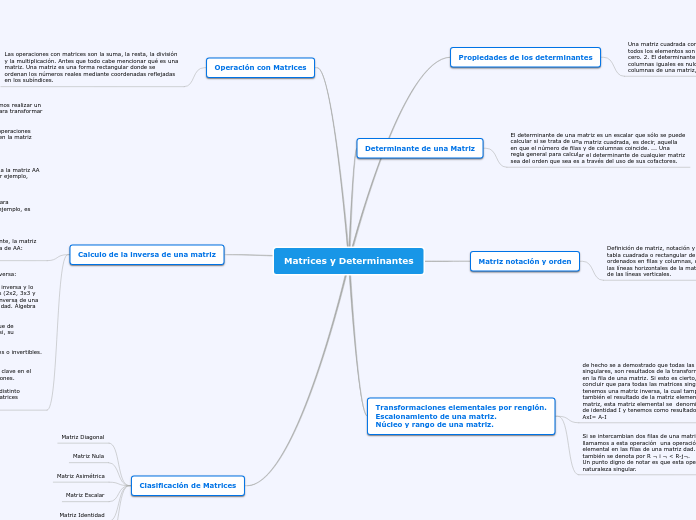
MAPA MENTAL
En el estudio de las funciones matemáticas, es crucial entender conceptos como el dominio y el rango. El dominio de una función se refiere al conjunto de todos los valores posibles de entrada que la función acepta.