door erika bravo 4 jaren geleden
551
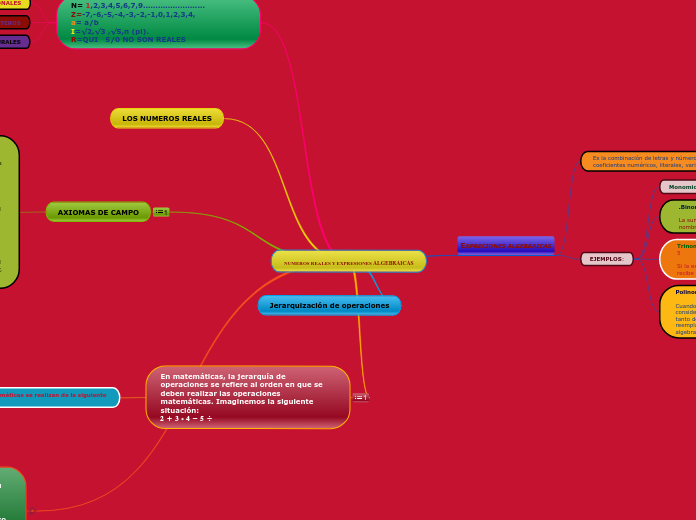
NUMEROS REALES Y EXPRESIONES ALGEBRAICAS
En matemáticas, es fundamental entender la jerarquía de operaciones para realizar cálculos correctamente. Esta jerarquía establece un orden específico para resolver sumas, restas, multiplicaciones y divisiones, asegurando resultados precisos.