av Dimas Cesar Balmaceda 2 år siden
196
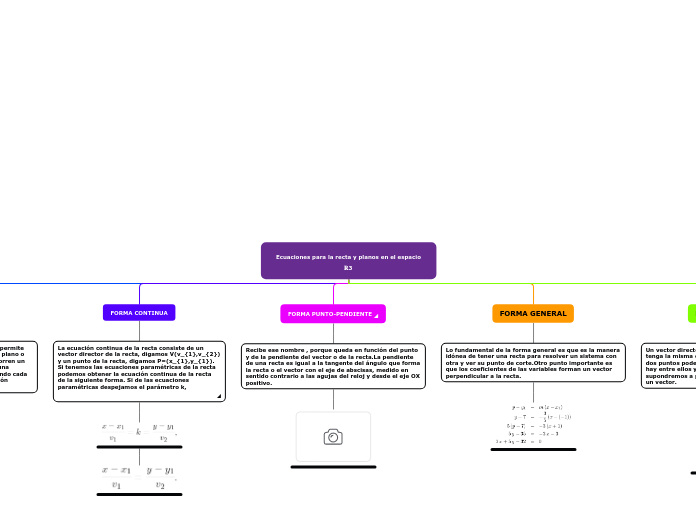
Ecuaciones para la recta y planos en el espacio 𝐑3
Existen varias formas de representar ecuaciones de rectas y planos en el espacio tridimensional. La forma punto-pendiente se basa en un punto y la pendiente del vector o de la recta, donde la pendiente es la tangente del ángulo que forma la recta con el eje de abscisas.