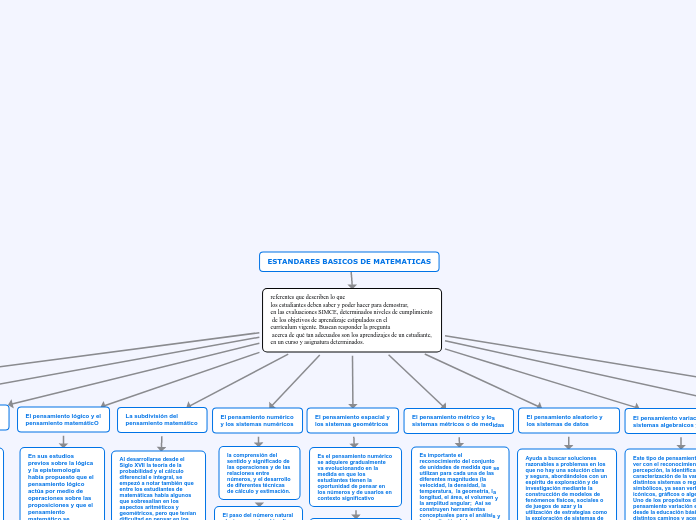
ESTANDARES BASICOS DE MATEMATICAS
referentes que describen lo que
los estudiantes deben saber y poder hacer para demostrar,
en las evaluaciones SIMCE, determinados niveles de cumplimiento
de los objetivos de aprendizaje estipulados en el
currículum vigente. Buscan responder la pregunta
acerca de qué tan adecuados son los aprendizajes de un estudiante,
en un curso y asignatura determinados.
Diseñar procesos de aprendizaje mediados por escenarios culturales y sociales
El aprendizaje se propone como un proceso activo que emerge de las interacciones entre estudiantes y contextos, entre estudiantes y profesores en el tratamiento de las situaciones matemáticas. Estas formas de interacción es interesante a la comunicación y la negociación, Por ello se enfatiza en el diseño de situaciones matemáticas que posibiliten a los estudiantes tomar decisiones; exponer sus opiniones y ser receptivos a las de los demás; generar discusión y desarrollar la capacidad de justificar la competencia.
Partir de situaciones de aprendizaje signifi cativo y comprensivo de las matemáticas
Las matemáticas escolares son situaciones que superan el aprendizaje pasivo, que generan contextos accesibles a los intereses y a las capacidades intelectuales de los estudiantes, les permiten buscar a formular estrategias de solución y usar productivamente materiales manipulativos y tecnológicos.
En la comunidad de educadores matemáticos se distingue hoy claramente entre situación y la actividad matemática necesita diferentes materiales didácticas para el trabajo intelectual personal y grupal de los estudiantes, tales como definir estrategias para interpretar, analizar, modelar y reformular la situación; producir, justificar, hoja de cálculo y transformar.
El pensamiento variacional y los sistemas algebraicos y analíticos
Este tipo de pensamiento tiene que ver con el reconocimiento, la percepción, la identificación y la caracterización de la variación y en distintos sistemas o registros simbólicos, ya sean verbales, icónicos, gráficos o algebraicos. Uno de los propósitos de cultivar el pensamiento variación es construir desde la educación básica Primaria distintos caminos y acercamientos significativos para la comprensión y la función de los sistemas analíticos, para el aprendizaje con sentido del cálculo numérico, geométrica y algebraica.
Los sistemas algebraicos es una forma muy apropiada de preparar el aprendizaje significativo y comprensivo de los sistemas algebraicos y su manejo simbólico mucho antes de llegar al séptimo y octavo grado. Estas actividades preparan a los estudiantes para la construcción de la expresión algebraica a través de la formulación verbal de una regla cursiva que muestre cómo construir los términos siguientes a partir de los precedentes y el hallazgo de un patrón que los guíe más o menos directamente a la expresión algebraica.
El pensamiento aleatorio y los sistemas de datos
Ayuda a buscar soluciones razonables a problemas en los que no hay una solución clara y segura, abordándolos con un espíritu de exploración y de investigación mediante la construcción de modelos de fenómenos físicos, sociales o de juegos de azar y la utilización de estrategias como la exploración de sistemas de datos, la simulación de experimentos y la realización de conteos.
En las experiencias cotidianas que los estudiantes ya tienen sobre estos sucesos y estos juegos, empiezan a tomar conciencia de que su ocurrencia y sus resultados son impredecibles e intentan realizar estimaciones intuitivas acerca de la posibilidad de aprender con números entre 0 y 1.
El pensamiento métrico y los sistemas métricos o de medidas
Es importante el reconocimiento del conjunto de unidades de medida que se utilizan para cada una de las diferentes magnitudes (la velocidad, la densidad, la temperatura, la geometría, la longitud, el área, el volumen y la amplitud angular; Así se construyen herramientas conceptuales para el análisis y la ejercitación de la equivalencia entre medidas expresadas en distintas unidades y la explicación de las relaciones pertinentes con el sistema de numeración decimal en sus diversas formas escriturales
El pensamiento espacial y los sistemas geométricos
Es el pensamiento numérico se adquiere gradualmente va evolucionando en la medida en que los estudiantes tienen la oportunidad de pensar en los números y de usarlos en contexto significativo
Esto requiere del estudio de conceptos y propiedades de los objetos en el espacio físico y geométrico en relación con los movimientos del propio cuerpo y las coordinaciones entre ellos y con los distintos órganos de los sentidos como la área, volumen, perímetro, métricos, medida y geometría.
El pensamiento numérico y los sistemas numéricos
la comprensión del sentido y significado de las operaciones y de las relaciones entre números, y el desarrollo de diferentes técnicas de cálculo y estimación.
El paso del número natural al número racional implica la comprensión de las medidas en situaciones en donde la unidad de medida no está contenida un número exacto de veces en la cantidad que se desea medir o en las que es necesario expresar una magnitud en relación con otras magnitudes.
Este paso de los números racionales a los números reales requiere del uso y comprensión de diferentes tipos de representaciones numéricas, sobre todo, las relativas a los números irracionales, tanto por medio de decimales infinitos como de símbolos algebraicos.
La subdivisión del pensamiento matemático
Al desarrollarse desde el Siglo XVII la teoría de la probabilidad y el cálculo diferencial e integral, se empezó a notar también que entre los estudiantes de matemáticas había algunos que sobresalían en los aspectos aritméticos y geométricos, pero que tenían dificultad en pensar en los conceptos de la probabilidad o en las variaciones continuas de los procesos físicos, como en el caso de longitud, área, métrico y volumen. la complejidad del símbolo (álgebra) y estadística.
El pensamiento lógico y el pensamiento matemáticO
En sus estudios previos sobre la lógica y la epistemología había propuesto que el pensamiento lógico actúa por medio de operaciones sobre las proposiciones y que el pensamiento matemático se distingue del lógico porque versa sobre el número y sobre el espacio,, dando lugar a la aritmética y a la geometría
La formulación, comparación y ejercitación de procedimientos
Esta reflexión exige al estudiante poder explicar y entender los conceptos sobre los cuales un procedimiento o algoritmo se apoya, seguir la lógica que lo sustenta y saber cuándo aplicarlo de manera fiable y eficaz, cuándo basta utilizar una técnica particular para obtener más rápidamente el resultado y el docente decida practicar y automatizar un solo algoritmo para cada una de las operaciones aritméticas usuales, es conveniente describir y ensayar otros algoritmos para cada una de ellas, compararlos con el que se practica en clase y apreciar sus ventajas y desventajas
Los cuatros procesos generales de la actividad matemática
suscitados por una situación problema permiten desarrollar una actitud mental perseverante e inquisitiva, desplegar una serie de estrategias para resolverlos, encontrar resultados, verifi car e interpretar lo razonable de ellos, modifi car condiciones y originar otros problemas.
La modelación es un sistema figurativo mental, gráfico o tridimensional que reproduce o representa la realidad en forma esquemática para hacerla más comprensible
La comunicación, en el que los estudiantes compartan el significado de las palabras, frases, gráficos y símbolos, aprecien la necesidad de tener acuerdos colectivos y aun universales y valoren la eficiencia y economía de los lenguajes matemáticos.
El razonamiento es un modelos y materiales físicos y manipulativos ayudan a comprender que las matemáticas no son simplemente una memorización de reglas y algoritmos, sino que tienen sentido, son lógicas, potencian la capacidad de pensar y son divertidas.
Sobre la noción de competencia matemática
es una sistemas y estructuras matemáticas como herramientas eficaces mediante las cuales se llevaban a la práctica determinados tipos de pensamiento lógico y matemático dentro y fuera de la institución educativa.
Las competencias que pueden asumir los niños y las niñas tienen que ver con las transformación que deben ser capaz de desarrollar la comprensión del conocimiento involucrado en cada una de las situaciones y problema, esta análisis se expresa tanto en los conceptos que son capaces de manipular consciente mente, como en las formas de proceder que usan apropiadamente.