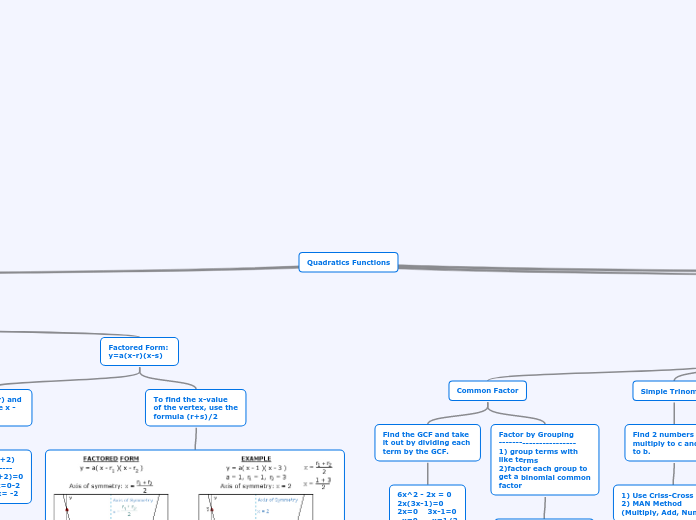
Solving Differential Equations
First Order DE
Integrate Directly?
No: try and separate
Separtable?
No: Try integrating Factor
Can be written in the form y'+P(t)=f(t)
No:Use Euler's Method
Yes: use integrating Factor
Yes: integrate and solve for y
Yes: Integrate and solve for y
Higher Order DE
Homogenous?
No:Find Homogenous and Particular Solution y(t) = yh(t) + yp(t) (Non-homogenous)
Any of the other used to find Homogenous solution
System of first order DE
Use Eigenvalues and Eigenvectors
Laplace Transformation
Yes: Find Homogenous Solution
Use Variation of Parameter
Use Undetermined Coefficients
Use Real Charaacteristic Roots
Check for repeated roots
Use Complex Characteristic Roots
General Solution
any IVP
No: find general solution
Yes: insert IVP into general solution