Organigrama arbol

Mer som dette

¿Qué es el Software y el Hardware?

Ved Verónica Vázquez García

IMPORTANCIA DEL CEREBRO

Ved evelin maya

Historia de las Matematicas

Ved ignacio vera

rocas igneas

Ved juliana roman

funciones reales

definicion

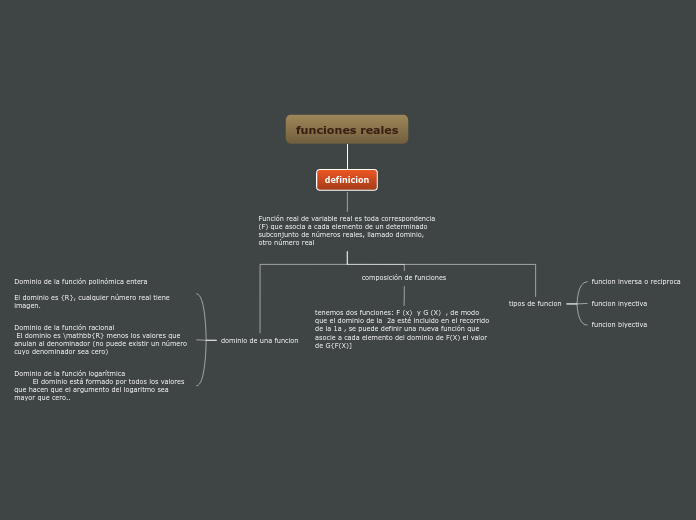
Función real de variable real es toda correspondencia (F) que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real

tipos de funcion

funcion biyectiva

funcion inyectiva

funcion inversa o reciproca

composición de funciones

tenemos dos funciones: F (x) y G (X) , de modo que el dominio de la 2a esté incluido en el recorrido de la 1a , se puede definir una nueva función que asocie a cada elemento del dominio de F(X) el valor de G{F(X)]

dominio de una funcion

Dominio de la función logarítmica El dominio está formado por todos los valores que hacen que el argumento del logaritmo sea mayor que cero..

Dominio de la función racional El dominio es \mathbb{R} menos los valores que anulan al denominador (no puede existir un número cuyo denominador sea cero)

Dominio de la función polinómica entera El dominio es {R}, cualquier número real tiene imagen.