av Valentina Torres 5 år siden
381
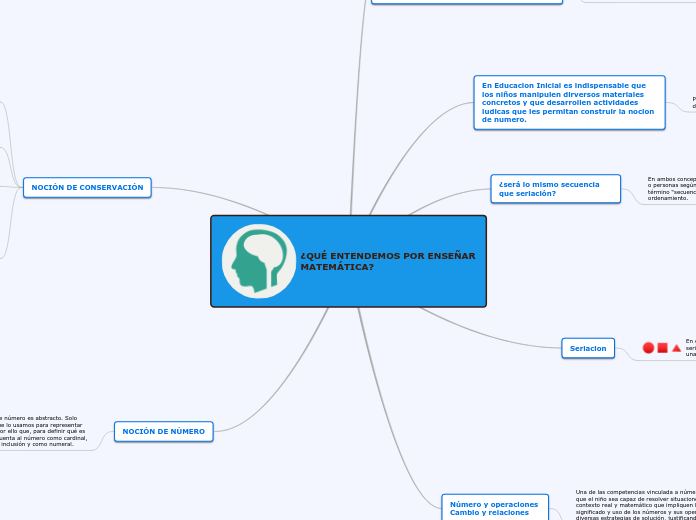
¿QUÉ ENTENDEMOS POR ENSEÑAR MATEMÁTICA?
La enseñanza de la matemática incluye la noción de conservación, que es la capacidad del niño para entender que ciertos atributos de los objetos permanecen invariables a pesar de cambios en su apariencia externa.