Statistics
Producing Data
Desinging Experiments
Cautions abut Experiment
lacking of realism limits ability to apply the conclusions of an experiment to the settings of greater interest
double-blind experiment
Design of Experiment
Do something to individuals in order to observe the response
Matched Pairs Design
more similar than unmatched subjects => more effective
compare tow treatments and the subjects are matched in pairs
an example of block design
Block Design
characteristics
allows to draw separate conclusions about each block
chosen based on the likelihood
can have any size
another form of control, which controls the effects of some outside variables by bring those variables into the experiment to form the blocks
formed based on teh most important unavoidable sources of variability among the experimental units
random assignment of units to treatments is carried out separately within a block
expected to systematically affect the response to the treatments
a group of experimental untis or subjects similar in some way
Randomizations
statistically significant
would rarely occur by chance
ovserved effect is very large
completely randomized design
all the experimental units are allocated at random among all treatments
randomized comparative experiment
ensure that influences other than the treatments operate equally on all groups
divide experimental units into groups by SRS
Replication
increase the sensitivity of the experiment to differences between treatments
reduce the role of variation
natural variability among the experiment units
Control
placebo
a dummy treatment
overall effort to mnimize variability in the way experimental unit are obtained and treated
reduce the problems posed by confounding and lurking variables
compares the responses in reatment group and control group
another group does not reveive any treatment (control group)
a group reveives the treatment
Desinging Samples
Cautions about Sample Surveys
Sampling Bias
response bias
the ordering of question may influence the response
respondent desires to please the interviewer
respondent may fail to understand the question
not give truthful responses to a question
wording bias
wording of the question influences the response in a systematic way
non-response bias
the possible biases of those who choose not to respond
persons who feel most strongly about an issue are most likely to respond
self-selected samples
Undercoverage
some part of population being sampled is somehow excluded
Multi-Stage Sampling Design
Cluster Sampling
all the individuals in the chosen clusters are selected to be in the sample
randomly select some of the clusters
divide population into groups as clusters
Probability Sample
Stratified Random Sampling
subgroups of sample, strata appear in approximately the same proportion in the sample as they do in the population
systematic sample
the rest are chosen according to some well-defined pattern
first member of the sample is chosen according to the some random procedure
Simple Random Sampling
4 steps to choose SRS
4 identify sample
3 stopping rule
2 table
1 label
every possibel sample is equally likely to be chosen
A sample of a given size
random sample
each member of the population is equally likely to be included
Designing Sample
Convenience Sampling
undercoverage bias
individuals who are easiest to reach
Voluntary response sampling
voluntary response bias
people who feel most strongly about an issue are most likely to respond
people who choose themselves by responding to a general appeal
Population and Sample
sample
sampling
may miss out centain characteristics of the population
advantages
less time needed
sampling involves studing a part in order to gain information about the whole
part of population that we actually examine in order to gather information
population
census
disadvantages
time causing
expensive
advantage
able to find all characteric of the population accurately
census attempts to contact every individual in the entire population
entire group of individuals
Observational Study & Experiment
experiment
allow to pin down the effects of specific variables of interest
observal the responses
deliberately impose some treatment on individual
Ovservational study
cheaper
explanatory variable is confounded with lurking variable
the effect of one variable on another often fail
do not attempt to influence the responses
observe individuals and measure variables of interest
Analyzing Data
More about Relationships between Two Variable
Establishing Causation
Explaning Causation
Explaing Association
Relationships between Categorical Variables
Simpon's Paradox
Transforming to Achieve Linearity
Power Law Model
Dependent variable = log(y) Independent variable = log(x) log(y)= b0 + b1log(x) ŷ = 10b0 + b1log(x)
Exponential Growth Model
Dependent variable = log(y) log(y) = b0 + b1x ŷ = 10b0 + b1x
Examining Relationships
Correlation and Regression Wisdom
Correlations Based on Averaged Data
Correlation: Measuring Linear Association
Least-Squares Regression
Lurking Variable
not among the explanatory or response variable in a study
Outliers and Influential Obserbation in Regression
Coefficient of Determination
r^2
% of observations lie on least squares regression line
Residuals & Residuals Plot
Std of residual
residual plot
should show no obvious pattern for liner relationship
how well the regression line fits the data
residual
observed y - predicted y
Scatterplots and correlation
Correlation
Least Squares Regression Line
y = a + bx
predict the value of y
Stright line describes how a response varible y changes sa an explanatory varible x changes
Does not measure curved relationship between variables
Measrue dircetion and strength of a linear relationship
r near to 1 or -1
strong linear relationship
r near to 0
weak relationship
Between -1 to 1
Categorical Variables in Scatterplots
Subtodisplay the different categories
different symbol
different plot color
Positive & Negative Association
Negative associate
above-average values of one tend to accompany below-average values of the other and vice versa
Positive associated
The above-average values and below-average value tend to occur together
Interpretion a Scatterplot
Describe the pattern by the direction, form and strenght of the relationship
Outlier: an individual value that falls outside the overall pattern of the relationship
Look for overall pattern and for striking deviations from that pattern
Plot the explanaory variable as the horizontal axis, and the response variable on the vertical axis
The relationship between 2 quantitative varibles measured on the same individuals
Response Variable and Explanatory Variable
Explanatory variable does not necessary causes the change in the response variable
To identify a response and explanatory variable by specifulying values of one variables in order to see how it affects another variable
An explanatory variable helps explain or influences changes in a response variable
A response variable measures an outcome of a study
Describing Location in a Distribution
Normal Distributions
Assesing Normallity
A normal probbility plot
Systematis deviations from a straight line indicate a non-Normal distribution
Outliers appear as points that are far away from the overall pattern of the plot
If the points on a Normal probility plot lie close to a straight line, the plot indicates the data are Normal
How well the data fit the empirical rule
Box plots
Stem plots
Histograms
Standard Normal Calculation
Standard normal table
Proportion of observations lie in some range of values
Standard Normal Distribution
For any Normal distribution we can perform a linear transformation on the variable to obtain an standard Normal distribution
A Normal distribution with mean 0 and standard deviation 1
Empirical Rule
Almost all (99.7%) of the values lie within 3 standard deviations of the mean
μ ± 3σ.
About 95% of the values lie within 2 standard deviations of the mean
μ ± 2σ.
About 68% of the values lie within 1 standard deviation of the mean
μ ± σ.
Normal Distribution
Importance
Many statistical inference procedures based on Normal distribution work well for other roughly symmetrical distributions
Good approximations to results of many chance outcomes
Often a good descriptor for some distribution of real data
Density function
These density curves are symmetric, single-peaked and bell-shaped
Mearures of Relative Standing and Density Curves
Position of the Score(How your score compares to other peoples's score)
Mean & Median of Density Curve
For different types of curves
Skewed lift: Mean is on the left side of the median
Skewed righta: Mean is on the right side of the median
Symmeric density curve: Mean = Median
Mean:"banlance point"
Median: "equal-areas point"
Density Curves
Mean and standard deviation
The area underneath is exactly 1
Always on or above and horizontal axis
Idealized description
A mathematical model for the distribution
Chebyshey's Inequality
In any distribution, the percentage of observations falling within standard deviation of the mean is at least
The pth percentil of a distribution is defined as the value with p percent of the ovservation less or equal to it
Z-Score
To measred how many standard deviations is avay from the mean
Exploring Data
Describing Distributions with Numbers
Comparing Distribution
Change Unit of Measures
Measuring Spread
Percentile
Box Plot
Interquartile range(IQR)
The difference between the first and third quartile
Q3, the 75 percentile
Q1, the 25 percentile
Median, M, the 50 percentile
Range:
difference between large and small observation
Mearuring the Center
Reisitant Measure
iThe median value is not affected by outlier values. Wd describe the median as a resistant measure.
Median
The Median is the middle number of a set of a data arranged in nmbrical ascending/descending order
NO. of items is ever
E.g:{3,5,9,10,15,15} Median = (9+10)/2
NO. of items is ole
E.g: {3.5,9,15,15},Median=9
Mean
The mean of a series of variables is the arithmetical average of those numbers
Displaying Distributions with Graphs
Shape of Graphical Displays
Bell-shaped
Uniformed
Skewed
Skewed right
Skewed left
Symmetric
Describing a Graphical Display
Outliers
Extreme values in the distribution
Due to natural variation in the data
Due to errors
Requires futher analysis
gaps
Holes in which no values fall into
Clusters
The natural subgroups in whch the values fall into
Spread
The scope of the valves from the smallest to the largest values
Center
The center which roughly separates the values roughly in hafl
Mode
The mode is one of the major "peaks" in a distribution
bimodal
Distribution with 2 mode
Unimodal
distribution with exactly one mode
Graphs for Quantitative Data
Time Plots
Cumulative Frequency Plots
Stemplots
Histrogram
Graphs for Categorical Data
Bar Chart
Pie Chart
Dotplots
Inference
Inference for Regression
Inference for Distribution of Catagorical Variables
Independence
The Chi-Square Test for homogeneity of populations
expected count = (row total*column total)/n
df = no. of catagoris-1
alternative hypothesis: at least one catagory data is different the null hypothesis
The Chi-Sqaure Distribution
The Chi-Sqaures Test fro Goodness of Fit
P-value and significant test
Comparing Two population Parameters
Indenpendence
SRS
Two sample tests about a population proportion
Population std unknown
The Two-Sample t procedure
Degree of Freedom
Choose the small one
software comput
two-sample t statistic
level C confidence interval
Population std known
Two-Sample z Statistic
Significance Tests in Pratice
The One-propottion z test
Normality condition
n(1-Po)≥10
nPo≥10
z = P-Po/√(Po(1-Po)/n)
The one sample t-test
Testing a Claim
P-value
Significant test
Type I and Type II error
If we fail to reject Ho when Ho is false, we have committed a type II error
power test
Increase the power of a test
Decrease std through improving the measurement process and restricting attention to a subpopulation
Increase the sample size
consider a particular alternative that is farther away from µ
increase alpha
The power of a test against any alternative is 1 minus the probability of a type II error for that alternative
1-ß
when a particular alternative value of parameter is true is called the power of the test againgst that alternative
If we reject Ho when Ho is actually true, we have a committed type I error
The significance level of any fixed level test is the probability of type I error
Use and Abuse of Tests
Beware of multile analyses
Statistical inference is not valid for all sets of data
Statistical Significance and Practical Importance
A statistically significant effect need not be parctically important
very small effects can be highly significan
choosing a Level of significance
increasing strong evidence as the P-value decrease
no sharp border between statistically significan and tattistically insignificant
What are the consequedces of rejecting Ho
How plausible is Ho
valued because an effect that is ulikely to occur simply by chance
Confidence intervals and Two-Sided Test
cannout use a confidence interval in place of a significance test for one-sided tests
in two-sided hypothesis test, a significance test and a confidence interval will yield the same conclusion
The link between two-sided significance tests and confidence interval is called duality
a two-sided significance test rejects a hypothesis exactly when the value µo falls outside a level 1- alpha confidence interval for µ
Test from confidene interval
if we are 95% confident that the true µ kues in the interval, we are also confident that the values of µ that fall outside ourinterval are incompatible with the data
intimate connection between confidence and significance and significance
porcedure
Step 4: Interpretation
Conclusion, connection and context
Interpret the P-value or make a decision about Ho using statistical significance
Step3: Calculations
Find the P-value
by GC
value used
µ≠µo, 2p
µ<µo, p
µ>µo, p
Calculate the test statistic
Step 2: Conditions: Choose the appropriate inference procedure
Sample follow Noraml distribution
Samples indenpendent from each other
Sample from SRS
t-Test for population mean
population std unknown
t = (x-µ)/(s/√(n))
z-Test for population mean
population std known
z = (x-µ)/(std/√(n))
Step1: Hypothesis
State hypotheses
Identity the population of interest and the parameter
Signficance tests are performed to determine whether the ovserved of a sample statistic differs significant from the hypothesized value of a population parameter
The probability of a result at least as far out as the result we actually got
Stating Hypohteses
alternative hypotheses
the claim about the population that we are trying to find evidence for
H0 : μ1≠μ2
null hypotheses
the statement being tested in a significance test
H0 : μ1 = μ2
Basic ideas
How rare is rare
An outcome that would arely happen if a claim were true is good evidence that the claim is not true
The basics
using a statistical test to asses the evidence provided by data about some claim concerning a populatin
using a confidence interval to estimate the population parameter
Estimating with confidence
Estimating a Population Proportion
Choosing the sample size
n=(z*/m)^2 p(1-p)
m = z*√(p(1-p)/n)
Conditions for Inference about a proportion
Normality
The datas are taken from SRS
level C confidence for population proportion: p±z*√(p(1-p)/n)
replace the standard deviation by the SE of p
Using the t procedures
large samples
Sample size less than 15, data close to normal
more important than the assumption that the population distribution is Normal
Robustness of t Procedures
not robuts against outliers
robust against non-Normality of the population
Paried t Procedures
The parameter µ is a paired t procedure is
the mean difference between before-and-after measurements for all individuals in the population
the mean difference in response to the two treatments fro individuals in the population
the mean difference in the responses to the two treatments within matched pairs of subjects in the entire population
compare the responses to the two treatments on the same sjubects, applys one sample t procedure
before-and-after measurement
matched pairs design
The One-Sample t confidence Intervals
The interval approximately correct fro large n in other cases
The interval is exactly correct when the population distribution is Normal
t* is the critical value for the t(n-1)
a level C confidence interval for µ is: x ± t*s/√n
unknown mean µ
The t Distribution
Density curves
density curve
as k increase. the denstiy curve approaches the N(0,1)curve ever more closely
The spread of the t distribution is a bit greater than that of the standard Normal distribution
similar in shape to the standard Normal curve
degree of freedom
write the t distribution with k degrees of freedom as t(k)
because we are using the sample standard deviation s in our calulation
df = n-1
Not normal, it is a t distribution
Extimating a Population Mean
Standard error of sample mean
*s stand for sample std
Conditions:
Individual observations are dndependent
Population have a normal distribution
Samples takne from SRS
Std of population unknown
How Confidence Interval Bheave and Determining Sample Size
Sample size
*E stand for margin of error
smaller margin of error
the sample size increase
the population standard deviation decrease
The confidence level C decreases
General Procedure for Inference with confidence Interval
Step 4: Interpret results in the context of the problem
Step 3: calculate the confidence interval
Step 2: Name the inference prodedure and check conditions
Step 1 : state the parameter of interest
Confidence interval for a Population Mean
Independence : population size is at least 10 tmes as large as the sample size
Normality: n is at least 30
sample taken from SRS
Confidence Interval
Confidence Interval and Confidence Level
Margin of error
z*std/√n
Standard error
std/√n
the estimated standard deviation of that percentage
the standard error of a reported proportion or percentage p measures its accuracy
The range of values to the left and right of the point estimate in which the parameter likely lies
for a parameter
gives the probability that the interval will capture the true parameter value in repeated samples
calculated from the sample data: statistic ± margin of error
Confidence interval
center
sample statistics
range of values
generated using a set of sample data
a range of plausible values that is likely to contain the unknown population parameter
Introduction
point estimate
a single value that has been calculated to estimate the unknwn parameter
Estimation
Porcess of determining the value of a population parameter from information provided by a sample statistic
Statistical inference
Provides methods fro drawing conclusions about a population from sample data
Probility and Ramdom Variables
Sampling Distributions
Central Limit Theorem
the mean and standard deviation of the sampling distribution is given by µ and std/√n
for large sample size n, the sampling distribution os x is approximately Normal for any population with finite std
Sample Means
standard deviation of sampling distribution = std/n
mean of sampling distribution = µ
Sample Proportions
a Normal approximation
n(1-p)≥10
np≥10
Only used when the population is at least 10 times as large as the sample
The standard deviation of the sampling disribution of p is given by √(p(1-p)/n)
The mean of sampling distribution of p is given by p
Bias and Variability
Variability
larger samples give smaller spread
determined by the sampling design and size of the sample
described by the spread of sampling distribution
To estimate a parameter is unbiased
The statistic is called an unbiased estimate of the parameter
The mean of its sampling distribution is equal to the true value of parameter being estimated
Sampling Distribution
the distribution of values taken by the statistic in all possible samples of the same size from the same population
Sampling Variability
The value of a statistic varies in repeated random sampling
Different samples will give different values of sample mean and proportion
Parameter & Statistic
Statistics comes from samples while parameters come from populations
A statistic is a number that can e computed from the sample data without making use of any unknown parameters
A parameter is a number that describes the population
The Binomial and Geometric Distributions
The Geometric Distributions
Calculating Geometric Probabilities
Geometric Mean and Standard Deviation
Varience = std^2 = (1-P)/p^2
Mean = 1/p
P(X=n) = (1-p)^(n-1)p
Geometric Distribution
The variable of interest, X, is the number of trials required to obtain the first success
The probability of a success, p is the same for each observation
The observations are all independent
Each observation falls into one of just two categories, "success" or "failure"
In a geometric random variable. X counts the number of trals until an event of interest happens
The Binomial Distributions
Normal Approximation to Bionomial Distribution
The accuracy of the Normal approximation improves as the sample size n increases
N(np, √np(1-p)
When n is large, the distribution of X is approximately Normal
The formula for binomial probabilities becomes awkward as the no. of trials n increase
Binomial Mean and Standard Deviation
Binomial Probability
Cumulative distribution function
cdf of X calculates the sum of probabilities for 0, 1, 2......, up to the value X
Probability distribution function
pdf assins a probability to each value of X
Binomial Formula
Binomial distribution is very important in statistics when we wish to make inferences about the proportion p of "success" in a popultaion
X~B(n,p)
X is binomially distributed with parameters n and p
X be the number of success after n trials
Binomail Distribution
Conditions
probility of success for each trial is the same
trials are independent
a fixed number n of trials
only 2 outcomes in each trial
The experiment is repeated a number of times independently
Two outcomes
Bernoulli distribution
Two possible outcomes: "success" or "failure"
p+q=1
q=P(failure)=1-p
p=P(success)
Random variables
Probability Density Function
Probility distribution
Condition
p(xi) = P(X=xi)
Means and Variances of Random Variables
standard deviation
variances
mean
Discrete and Continuous Random Variables
continuous random variable
random variable that assumes values associated with one or more intervals on the number line
discrete random variable
random variable with a countable number of outcomes
Probability distribution
a list of the possible values of the DRV together with their respective probabilities
random varible X
A numerical value assigned to an outcome of a random phenomenon.
Probability and Simulation
General Probability Rules
Probability Tree
Conditional probability
A given B
Probability Models
Important Probability Results
indenpendent event
chance of one event happen or does not happen doesn't change the probability that the other event occurs
P(A and B) = P(A) * P(B)
two events A and B are disjoint
mutually exclusive
complement rule
Probability("not" an event) = 1 - Probability(event)
P(S) = 1
P(A)= 0, event A will never occur
P(A) =1, event A will certainly occur
0≤P(A)≤1
Probility of an Event with Equal Likely Outcomes
P(A) = n(A)/s(A)
probility modal
a mathematical description of a random phenomenon consisting of two parts
a way of assigning probabilities to event
a sample space S
event
any outcome or a set of outcomes of a random phenomenon
Sample space
S
the set of all possible outcomes
Simulation
The Idea of Probability
random
probability of any outcome of a random phenomenon is the proportion of times the outcome would occur in a very large series of reptitions
a regular distribution of outcomes in a large no. of repetitions
individual outcomes are uncertain
chance behavior is unpredicatable in the short run but has a regular and predictable pattern in the long run
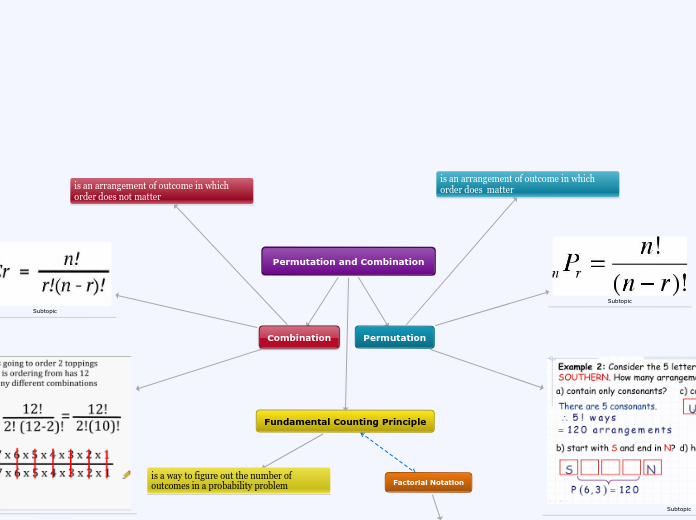
Permutation & Combination
Circular permutation
Subtopic
we have (n-1)! wys to arrange n distinct objects in a circle
each object has two "neighbors" when arranged in a circle
Conbination
nCr
there are c ways of selecting r objects
order is not important
Permutation
if there are n objects in total with p identical objects, we have n!/p! ways of arranging all the objects in a row
if some of the objects are identical, the no. of permutations will be less
if we choose r objects from n distinct objects, wer have nPr ways to arranging the r objects
if there are n distincts objects. we have n! ways of arranging all the objects in a row
The ordir of the objects is important
a permutation is the arrangement of objects taken from a ser
Addition and Multiplication Principle