av MALAK THAINA 2 år siden
185
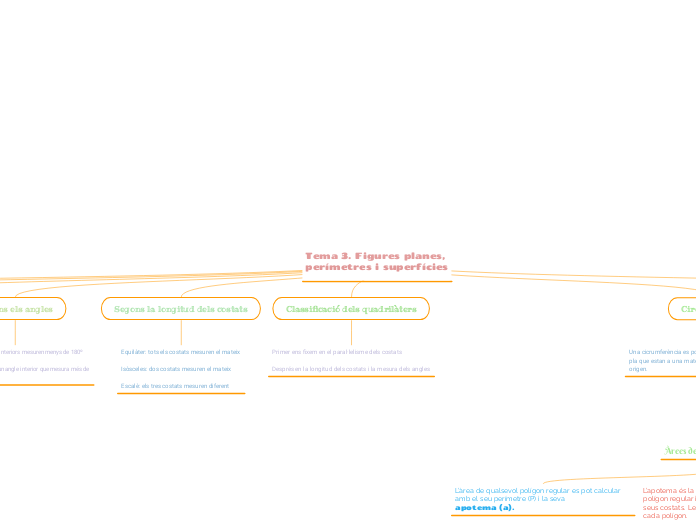
Tema 3. Figures planes, perímetres i superfícies
Un polígon es defineix com una figura geomètrica plana tancada formada per costats rectes y vèrtexs. Els polígons es poden classificar segons el nombre de costats, la longitud dels mateixos, i els seus angles.