av Larimar Machado sarang 3 år siden
180
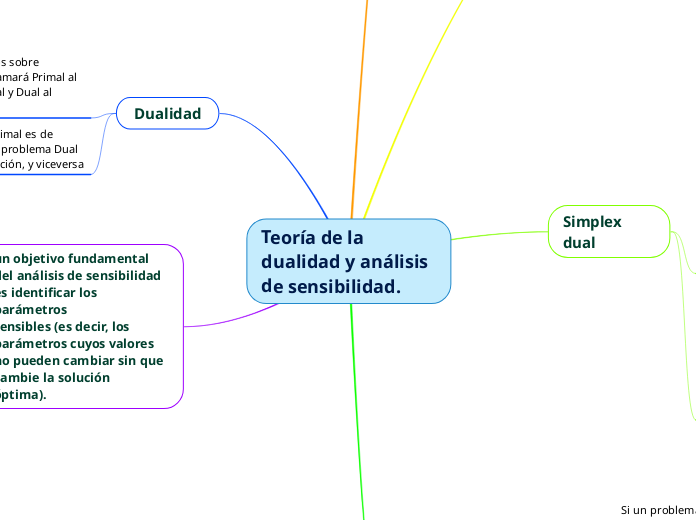
Teoría de la dualidad y análisis de sensibilidad.
La teoría de la dualidad en programación lineal explora la relación entre dos problemas, el Primal y el Dual. Estos problemas están intrínsecamente conectados; si uno tiene soluciones factibles y una función objetivo acotada, el otro también.