por leiddy cardona 1 ano atrás
154
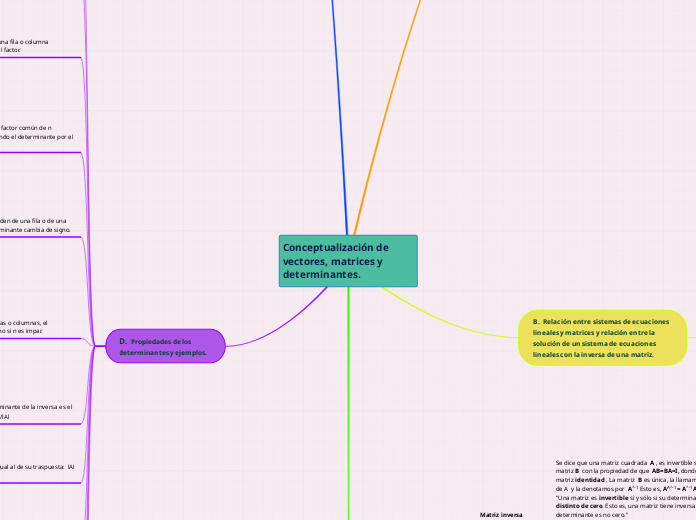
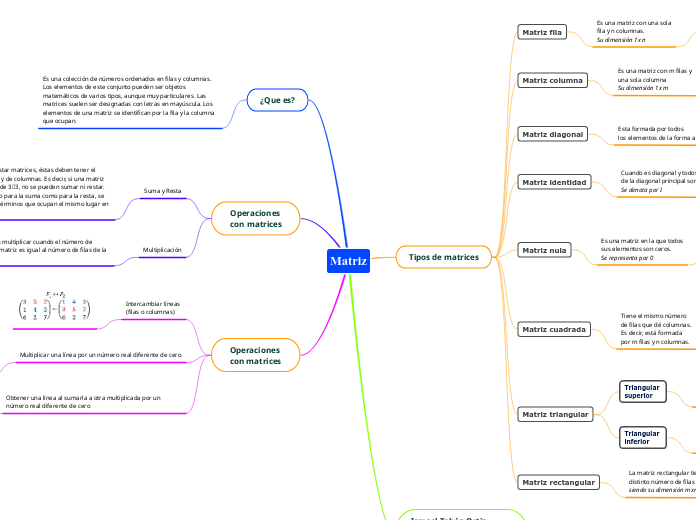
Conceptualización de vectores, matrices y determinantes.
En el ámbito del álgebra lineal, se estudian conceptos fundamentales como vectores, matrices y determinantes. Las propiedades de los determinantes juegan un papel crucial en la comprensión de las matrices.