Geometry/Measurement Project
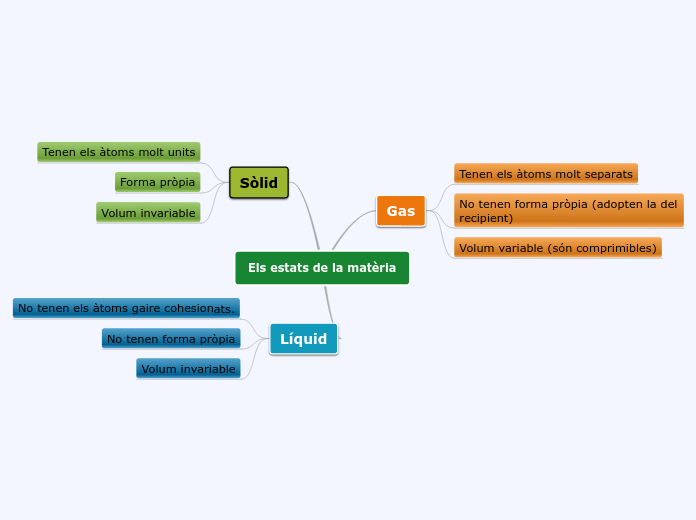
Area
Area of a rectangle: length times width
Area of a parallelogram: base times height
Area of a triangle: 1/2 times base times height
Area of a trapezoid: 1/2 (base A + base B) times H
The area of a circle
Area is the surface size of a figure. Area is always expressed in units squared.
Pythagorean Theorem
The equation for the Pythagorean Theorem is a^2+b^2=c^2
The pythagorean theorem only works for right triangles, therefore you can determine if triangle is right by plugging the numbers into the equation
Lets say A=2 B=5 and C=10
2^2+5^2 = 10^2, 4+25=100, or 29=100. This is incorrect, therefore you have identified that this triangle is not a right triangle.
In this example lets say A=3 B=4 and C is unknown
You would solve "C" by using the equation, 3^2+4^2=C^2, you would then get 9+16=C^2, 25=C^2, C=5 units
It is important to remember "C" is always the hypotenuse of the triangle
Surface Area
You can always just add up the area of all the sides, but there are some equations and tricks to avoiding the hassle and uncertainty of that!
Surface area is the sum of the lateral surface areas and the area of the bases
Equations
Sphere
4piR^2
When radius =3, 4pi(3^2), 4pi(9), 36piUnits^2
Cone
piR^2+piRXs
In this equation S=slant height and R=Radius of the base
A cone with a slant height of 4, and a radius of 6 would be pi6^2+pi6X4, 36pi+24pi=60piUnits^2
Pyramid
B+1/2ps
In this equation B=the area of the base, p=number of sides and s=slant height
For example a pyramid with four sides, a slant height of 3, and a base area of 12 would be, 12+1/2(3X4), 12+6, 18Units^2
Cylinder
This equation is similar to the prism, only the area of the base would be circular, therefore the "2b" become "2piR^2" and the "PH" becomes "2piRXH"
A cylinder with Radius 2 and Height 4 would be, 2pi(2^2)+ 2pi2X4, 8pi+16pi, or 24pi (Units^2)
Prism
PH+2B
This equation takes a lot of explaining, for example P=the perimeter of the base, H=the height of the prism, and B=the AREA of the base
An example would be, P=12, H=10, and B=6. The equation would then be (12X10)+(6X2)- resulting in an answer of 132Units^2
Cube
6(eXe)
, for a cube with side lengths of 5, you would solve it like so 6(5X5), 6(25), The surface area is 150 Units^2
Prisms
You can easily tell the shape of a prism by its name. For example a triangle right prism has 2 triangle bases meaning there are three sides that have a right angle. A hexagonal oblique prism will be tilted and not have any right angles at all because it is hexagonal we know that it has 6 sides.
An oblique prism has lateral faces that are NOT perpendicular to the faces.
The right prism has two lateral faces that are perpendicular to the bases.
If you are looking at a 2 dimensional figure you can still visulize a prism and define the characteristics.
-you can determine this by the amount of sides and name them from that amount of sides. For example the picture below you can see the bases are triangles and the sides are rectangles even tho the picture is only 2 dimensional.
Subtopic
A prism has 2 congruent faces (the bases) in parallel planes and other faces (lateral faces) bounded by parallelograms
Perimeter
Circumference is the name of the perimeter of a circle. The equation is C= 2*pi*r where r is the radius. This also means that C=2pi*r
Perimeter is the distance around a plane figure where you add up all of the sides.
Volume
Polyhedron: a three-dimensional figure made up of sides called faces, each face being a polygon
To determine the volume of a polyhedron, follow the steps below:
1. center the polyhedron at the orgin of the 3-dimensional rectangular coordinate system
2. draw lines from each vertex (corner) to the orgin. Each face is now the base of a pyramid with the orgin as its apex.
3. Calculate the volume of each pyramid. Using pyramids volume formula ( V=(1/3)B*h where B is the area of the base.
4. Add together the volumes of all the pyramids to get the entire volume of the polyhedron.
Volume of a pyramid
Volume of a cone
Volume of a prism
Volume of a cylinder
Volume of a cube
The volume of a figure is the number of cubes required to fill it completely. Volume is measured in "cubic" units. An easy way to understand and remember volume is by listening to the volume song for kids: http://www.youtube.com/watch?v=JijhDDJvExo
Types of Polygons, Triangles, Quadrilateral, and Circles
Circle- This shape is different because it does not have any sides.
A regulare polygon is a convex polygon that is both equilateral and equiangular
Quadrilaterals is any shape that has 4 sides
A square has all the sides are the same length and all right angles.
A rectangle is a parallelogram with all right angles.
A rhombus is a parallelogram with all the sides of the same length.
A parallelogram has two pairs of opposite parallel sides
Isosceles Trapezoid has two sides parallel and two congruent angles
A trapezoid has two parallel sides
A kite has two pairs of adjacent congruent sides
Triangle
Equilateral- All three sides have to be the same length
Isosceles- At least two sides of the triangle have the same length sides
Scalene- No two sides of the triangle have the same length
Obtuse Triangle-If an interior angle is obtuse (if the angle is greater than 90°)
Right Triangle- if one angle is a right angle ( the angle equals 90°)
Acute Triangle- all three interior angles are acute (the angles have to be less than 90°)
Polygon- Is a simple closed polygonal curve.
Pentagon has 5 sides
Quadrilateral has 4 sides
A triangle has 3 sides
Geometric Figures
Sum Of Angles For A Triangle- All three angles should add up to 180°.
Classification of Angles-
Straight Angle- a line segment that equals 180°
Acute Angle- Two line segments that have an angle less then 90°
Obtuse Angle- Two line segments that have an angle greater than 90°
Right Angle- two line segments that have an angle of 90°
Corresponding Angles- When two lines are crossed by another line, the angles in matching corners are called corresponding angles.
Angle Measure- the number of degrees of turn to rotate about the vertex
Congruent Angles- These are two angles that have the same measure
Supplementary Angles- Two angle sums that add up to 180°
Corresponding Angles- Two angle sums that add up to 90°
Angle- The point when two line segments meet
together