por christopher chacon 3 anos atrás
247
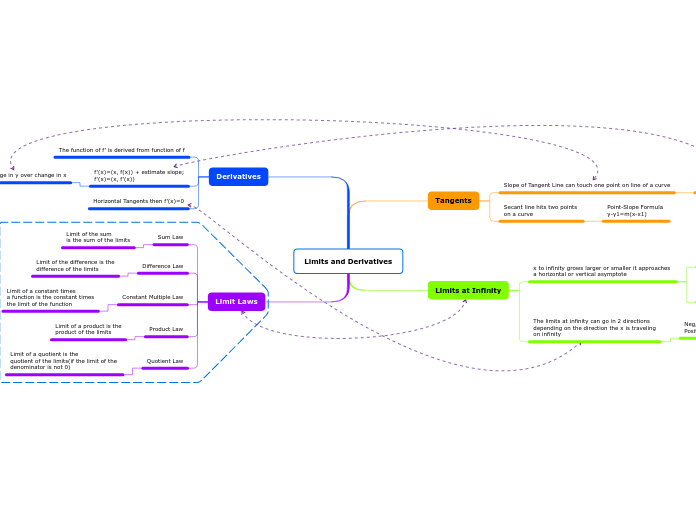
Limits and Derivatives
Calculus involves the study of limits and derivatives, fundamental concepts that help describe how functions behave. Limits are used to determine the behavior of a function as it approaches a particular point or infinity, with various laws such as the Product, Quotient, Sum, Constant Multiple, and Difference laws governing their calculations.