por VALERIA PEREZ CASTILLO 3 anos atrás
178
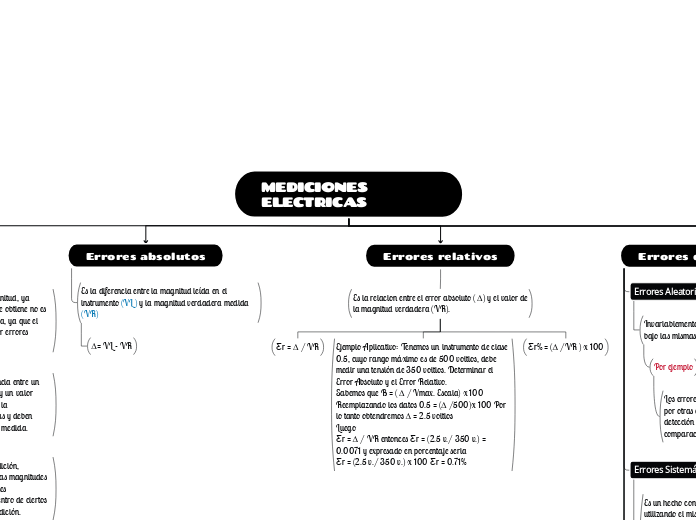
MEDICIONES ELECTRICAS
En el ámbito de las mediciones eléctricas, el término 'error' no lleva las connotaciones negativas habituales, sino que se refiere a la incertidumbre inherente en cualquier medición.
por VALERIA PEREZ CASTILLO 3 anos atrás
178

Mais informações
Se utilizan en aparatos de medida magnetoeléctricos de cuadro móvil y en aparatos de medida electrodinámicos cuando se emplean como medidores de potencia.
Figura de escalas
Con zona muerta
Comprimida
Fraccionada
Cuadratica
Lineal
Por ejemplo
Los errores de calibración de escalas, en general, por otras causas medibles con precisión. La detección y corrección de estos errores se efectúa por comparación o contraste con instrumentos patrones.
Los fabricantes de instrumento de medición, garantizan que los valores reales de las magnitudes medidas, en condiciones experimentales determinados, están comprendidos dentro de ciertos limites referidos al resultado de la medición.
En toda medición existe error. Si la precisión del equipo de medida es el conveniente, independientemente de su exactitud, siempre se observara una discrepancia entre los resultados de dos medidas.
La palabra "discrepancia" no es sinónimo de "error".
Por ejemplo la discrepancia entre el valor medido para la resistencia por unidad de longitud de un hilo de cobre estándar y el valor que aparece en las tablas no es necesariamente un error de medida. Las características del cobre utilizado para este experimento pueden ser diferentes de las del utilizado para confeccionar las tablas.
Si dos personas obtienen resultados diferentes para la misma cantidad se puede decir que existe discrepancia entre ambos resultados, pero el error introducido por cualquiera de ellos puede ser mayor que dicha discrepancia.
La incertidumbre es la "duda del metrólogo" acerca de la calidad o exactitud de la medición realizada, la cual, cuantifica a fin de comunicarse con sus homólogos. Un valor medido no tiene incertidumbre el que la tiene es quien realizo la medición y a fin de comunicación.
Se debe prestar atención y tener clara la diferencia entre error e incertidumbre.
Por ejemplo el resultado de una medicion luego de aplicar una correcion (por los errores sistematicos) pueden estar muy cerca dl valor de la cantidad, aunque no lo odemos saber, es decir con un error pequeno, aunque puede existir, debido a los metodos e instrumentos utilizados en la medicion, una gran incertiurmbre.
Cuantitativamente el error de medida se expresa, normalmente, utilizando una medida acertada de la incertidumbre que se define matemáticamente. La mas corriente de tales medidas en el trabajo científico es la desviación del patrón (desviación estándar). En otras mediciones se consideran otro tipo de desviación. La repetición de una medida bajo las mismas condiciones nunca dará el mismo resultado.
Hay dos razones principales para estudiar el error de medida.
Estudiar como puede calcularse la veracidad de los resultados.
Hallar la forma de reducirlos