por Montana Ebbesen 6 anos atrás
342
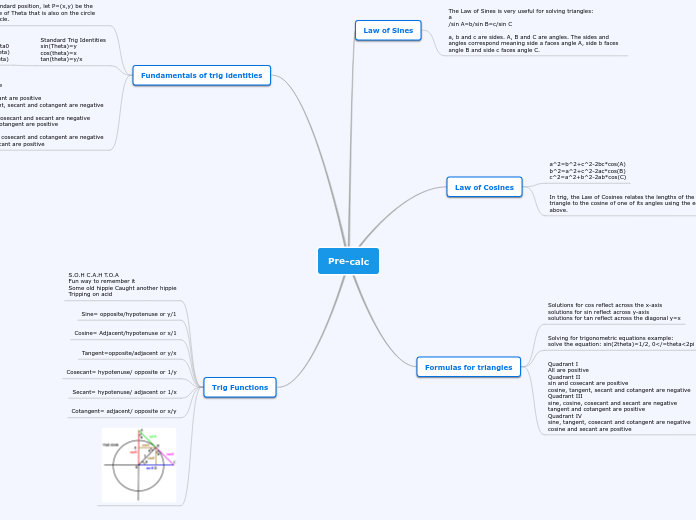
Pre-calc
The Law of Cosines is a fundamental trigonometric principle that connects the lengths of a triangle's sides with the cosine of one of its angles. Various equations express this relationship, such as a^2 = b^2 + c^2 - 2bc *