por Julia Santos 9 anos atrás
376
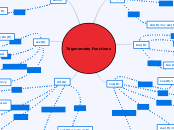
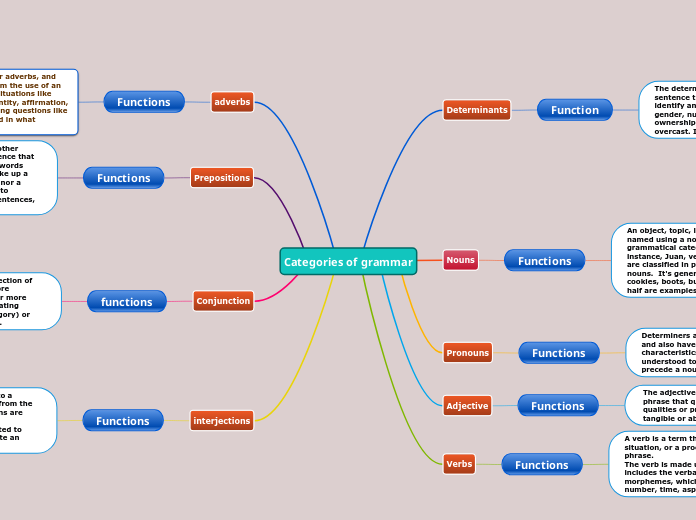
Six Trig Functions
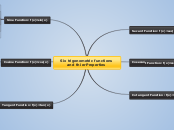
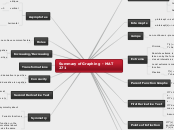
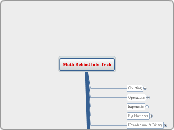
Trigonometric functions describe relationships between angles and sides of triangles. The primary functions include sine, cosine, tangent, cotangent, secant, and cosecant. Each function has a unique graph that represents its behavior.