realizată de Lizzie Ortiz 4 ani în urmă
224
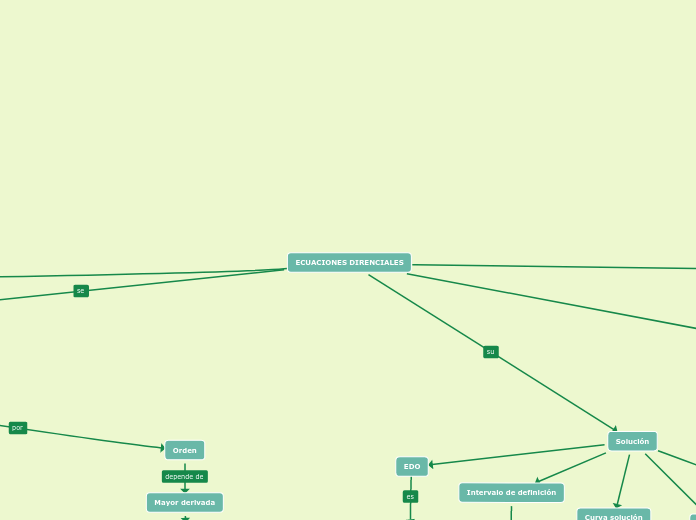
ECUACIONES DIRENCIALES
Las ecuaciones diferenciales pueden clasificarse en ecuaciones diferenciales ordinarias (EDO) y ecuaciones diferenciales parciales (EDP). Las EDO involucran derivadas con respecto a una sola variable independiente, mientras que las EDP incluyen derivadas con respecto a múltiples variables independientes.